Tuning velocities and anisotropy ratios
Module: tutorials.02_EP_tissue.03A_study_prep_tuneCV.run
Section author: Caroline Mendonca Costa <caroline.mendonca_costa@kcl.ac.uk>
Concept
This tutorial introduces the theoretical background for the relationship between conduction velocity and tissue conductivity and how a iterative method to tune the conductivity values to yield a desired velocity for a given setup can be derived. In addition, the definition of anisotropy ratio and its impact on simulation results are presented. A simple strategy to enforce desired anisotropy ratio and conduction velocities is also presented.
Tuning Conduction Velocity
The relationship between conduction velocity and conductivity
A minimum requirement in modeling studies which aim at making case-specific predictions on ventricular electrophysiology is that activation sequences are carefully matched. Conduction velocity in the ventricles is orthotropic and may vary in space, thus profoundly influencing propagation patterns.
As described in Section [Tissue scale],
the monodomain model [1]
is equivalent to the bidomain model [2]
if the monodomain conductivity tensor is given by the harmonic mean tensor, 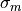
(32)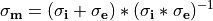
Conduction velocity, CV , is not a parameter in the bidomain equations
[2] and as such cannot be directly
parametrized. However, assuming a continuously propagating planar wavefront along a given direction,  ,
one can derive a proportionality relationship [1] between
,
one can derive a proportionality relationship [1] between  and
and 
(33)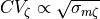
Note
For simplicity, the surface-to-volume ratio, 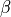 , was ommited in this tutorial,
as it is kept constant when tuning conductivities [1]
, was ommited in this tutorial,
as it is kept constant when tuning conductivities [1]
Conduction velocity as a function of simulation parameters
Experimental measurements of conductivity values are scarce and the variation in
measured values across studies is vast. These uncertainties inevitably arise due to the significant degree of
biological variation and the substantial errors in the measurement techniques themselves.
Modeling and technical uncertainties may also have an
impact on model predictions. Particularly, CV depends on the specific model used to describe cellular dynamics, 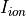 ,
the spatial discretization,
,
the spatial discretization, 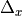 , and on several implementation choices including the time-stepping scheme used, which
we represent as
, and on several implementation choices including the time-stepping scheme used, which
we represent as 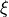 . Thus, CV can be represented as a function
. Thus, CV can be represented as a function
(34)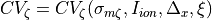
Iterative scheme for conduction velocity tuning
In most practical scenarios, 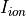 ,
, 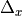 , and
, and 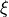 are parameters defined by users in the course of
selecting a simulation software, an ionic model and a provided mesh to describe the geometry. Thus, only
are parameters defined by users in the course of
selecting a simulation software, an ionic model and a provided mesh to describe the geometry. Thus, only 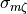 is left
which can be tuned to achieve a close match between the pre-specified conduction velocity,
is left
which can be tuned to achieve a close match between the pre-specified conduction velocity, 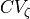 , and the velocity,
, and the velocity, 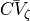 ,
predicted by the simulation.
,
predicted by the simulation.
Using (33), and (32) one can find unique monodomain conductivities along all
axes 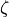 , which yield the prescribed conduction velocities,
, which yield the prescribed conduction velocities, 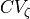 ,
by iteratively refining conductivities based on
,
by iteratively refining conductivities based on 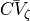 ,
measured in simple 1D cable simulations. The iterative update scheme we propose is given as
,
measured in simple 1D cable simulations. The iterative update scheme we propose is given as

Fig. 63 Iterative update scheme to tune conductivity values based on a prescribed velocity 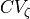 [1]
[1]
The algorithm is implemented as follows. Given an initial conductivity “guess”, 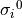 and
and 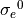 and all other
simulation parameters defined by
and all other
simulation parameters defined by 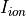 ,
, 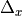 , and
, and 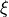 , a simulation is run using a
1D cable and the conduction velocity is computed, as described in the figure below:
, a simulation is run using a
1D cable and the conduction velocity is computed, as described in the figure below:
Fig. 64 Setup for convergence testing. A pseudo 1D cable is created, which is in fact a 1 element tick cable of hexahedral elements,
where  is the edge length of each hexahedral, which also defines the spatial resolution.
Propagation is initiated by applying a transmembrane stimulus current at the left corner.
is the edge length of each hexahedral, which also defines the spatial resolution.
Propagation is initiated by applying a transmembrane stimulus current at the left corner.
 , and
, and 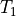 correspond to wavefront
arrival times recorded at locations
correspond to wavefront
arrival times recorded at locations 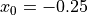 cm and
cm and 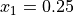 cm,
respectively. CV is computed as
cm,
respectively. CV is computed as 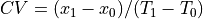 .
.
Using 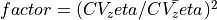 , the conductivities
, the conductivities ![{\sigma_i}[i+1]](../../_images/math/5242fbc2ac0e5b0a158abc2dcda505998be2e557.png) and
and ![{\sigma_e}[i+1]](../../_images/math/b4b3751ba64395c5bbe71841edad816d41cfdd37.png) are updated. A new simulation is then run with the new conductivities.
These steps are repeated until the error in CV is below a given tolerance,
are updated. A new simulation is then run with the new conductivities.
These steps are repeated until the error in CV is below a given tolerance, 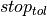
Problem Setup
This tutorial will run a simulation on a 1D cable and compute the simulated CV, 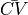 , and/or run
the iterative scheme shown Figure Fig. 63 to compute the conductivity
, and/or run
the iterative scheme shown Figure Fig. 63 to compute the conductivity 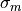 which yields
the prescribed CV for the chosen simulation setup.
which yields
the prescribed CV for the chosen simulation setup.
Usage
The experiment specific options are:
--resolution RESOLUTION
Spatial resolution
--velocity VELOCITY Desired conduction velocity (m/s)
--gi GI Intracellular conductivity (S/m)
--ge GE Extracellular conductivity (S/m)
--ts TS Choose time stepping method. 0: explicit Euler, 1:
crank nicolson, 2: second-order time stepping
--dt DT Integration time step on micro-seconds
--converge {0,1} 0: Measure velocity with given setup or 1: Compute
conductivities that yield desired velocity with given
setup
--compareTuning run tuneCV with --resolution 100 200 and 400 with and
without tuning and make comparison plot
--compareTimeStepping
run tuneCV with --resolution 100 200 and 400 with
Explicit Euler and Crank Nicolson and make comparison
plot
--compareMassLumping run tuneCV with --resolution 100 200 and 400 with and
without mass lumping and make comparison plot
--compareModelPar run tuneCV with --resolution 100 200 and 400 with
original Ten Tusher cell model and with reduced
sodium conductance and make comparison plot
--ar AR run tuneCV with for CV_f = 0.6 and CV_s = 0.3 m/s with
given anisotropy ratio (ar)
The user can either run single experiments, do a comparison of the multiple
resolutions with the options --compareTuning, --compareTimeStepping, --compareMassLumping, and --compareModelPar,
or compare the change in conductivities with different anisotropy ratios
Run 1D examples
To run the experiments of this tutorial do
cd ${TUTORIALS}/02_EP_tissue/03A__study_prep_tuneCV
compareTuning:
To compute the conductivities for resolutions of 100, 200, and 400 um with and without tuning, run:
./run.py --compareTuning --visualize
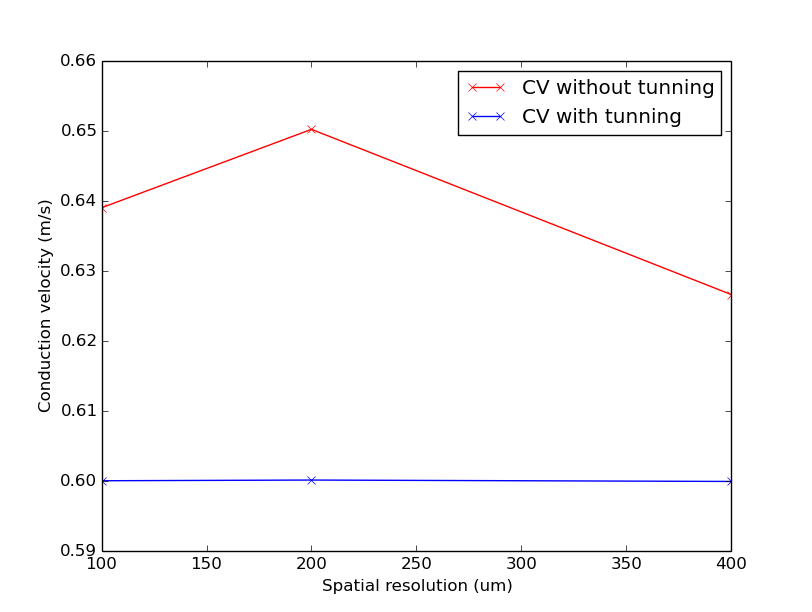
After running this command you should see the following plot
Note
Notice that CV varies with resolution in a non-linear fashion and CV is constant when the iterative scheme is applied.
compareTimeStepping:
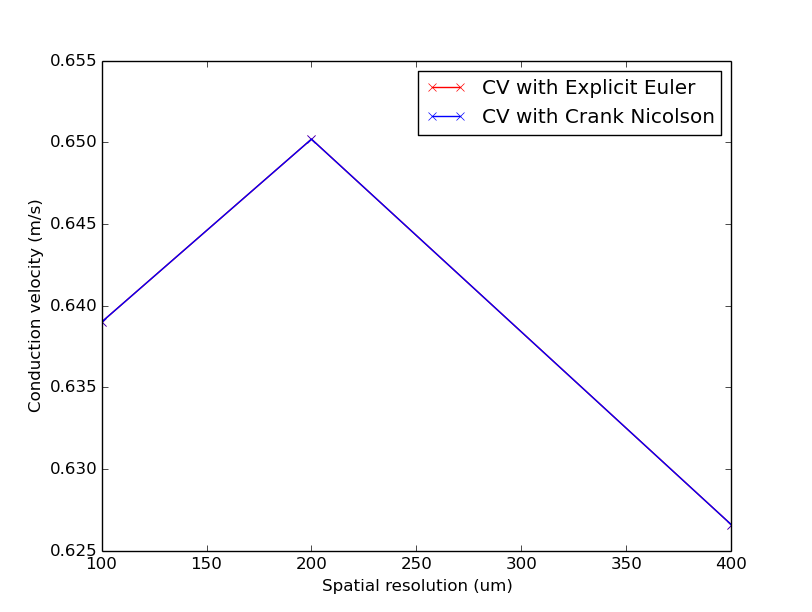
To compare the effect using the Explicit Euler or Crank Nicolson methods for the resolutions of 100, 200, and 400 um run:
./run.py --compareTimeStepping --visualize
Note
Notice that CV varies with resolution virtually identically with both time-stepping schemes.
compareMassLumping:
Mass lumping is a common numerical technique in FEM to speed up computation. The mass matrix, 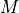 , is made diagonal,
implying that its inverse is also diagonal, and solving the system is trivial.
The lumped mass matrix,
, is made diagonal,
implying that its inverse is also diagonal, and solving the system is trivial.
The lumped mass matrix, 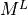 , is computed by setting its main diagonal to be
, is computed by setting its main diagonal to be
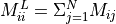
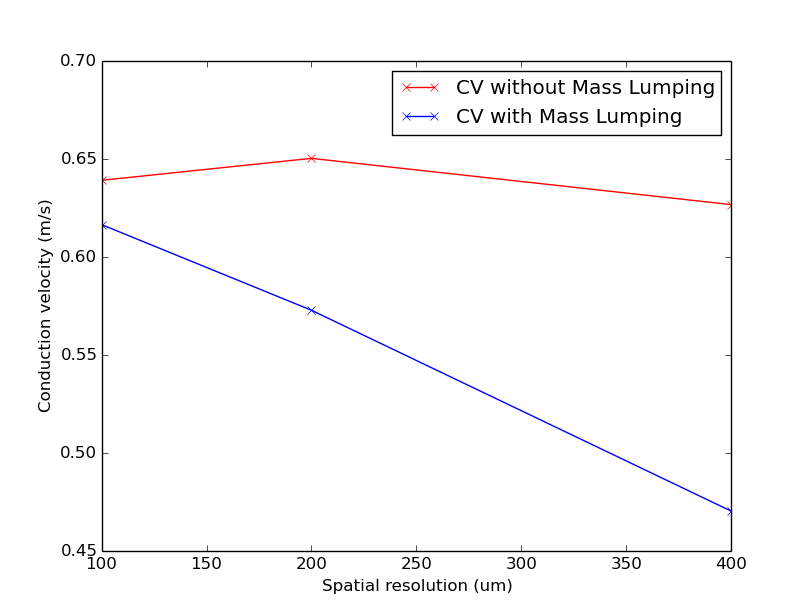
To compare the effect of using mass lumping on CV for the resolutions of 100, 200, and 400 um run:
./run.py --compareMassLumping --visualize
Note
Notice that CV varies with resolution in both cases, but the decrease in CV for coarser resolutions is much steeper with mass lumping.
compareModelPar:
To compare the effect of modifying the sodium conduction on CV for the resolutions of 100, 200, and 400 um run:
./run.py --compareModelPar --visualize
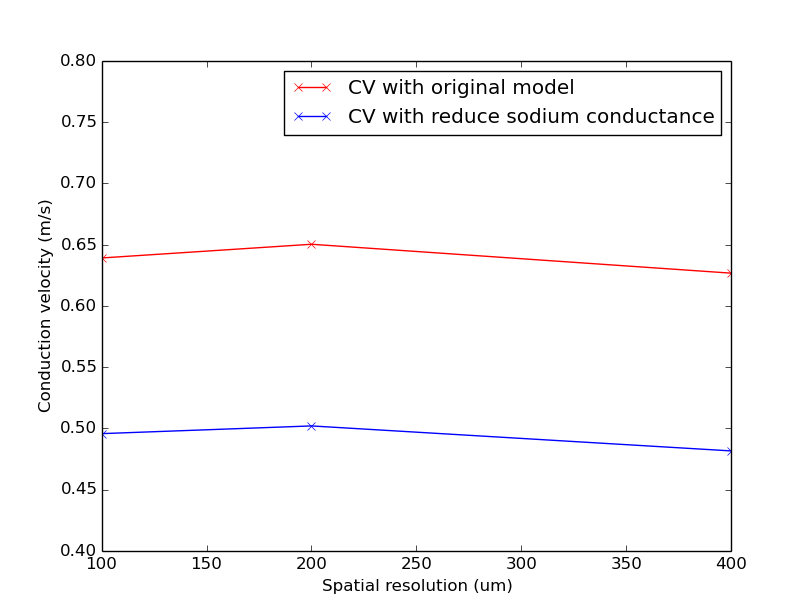
Fig. 68 Simulated CV for different resolutions with the original Ten Tusher model and with reduce sodium conductance
Note
Notice that CV varies with resolution similarly in both cases, but the CV with reduced sodium conductance is lower than with the original model.
Run 2D and 3D examples
As previously mentioned, conduction velocity in the ventricles is orthotropic, that is, CV is different
in each axis 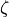 . Estimated average CVs in the longitudinal, transverse, and sheet normal directions,
. Estimated average CVs in the longitudinal, transverse, and sheet normal directions,
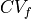 ,
, 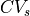 and
and 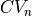 , are about 0.67 m/s, 0.3 m/s, and 0.17 m/s, respectively [2].
, are about 0.67 m/s, 0.3 m/s, and 0.17 m/s, respectively [2].
2D:
To run a 2D simulation where 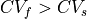 , that is, an anisotropic setup, two sets of conductivities must be defined,
one for each axis
, that is, an anisotropic setup, two sets of conductivities must be defined,
one for each axis 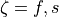 . To compute two sets of conductivities with tuneCV, call the example without
the “compare” flags twice with two different velocities and look at the conductivities output in the screen
. To compute two sets of conductivities with tuneCV, call the example without
the “compare” flags twice with two different velocities and look at the conductivities output in the screen
For the longitudinal direction, run
./run.py --velocity 0.6 --converge 1
You should get an output close to the following:
Conduction velocity: 0.6398 m/s [gi=0.1740, ge=0.6250, gm=0.1361]
Conduction velocity: 0.6006 m/s [gi=0.1530, ge=0.5497, gm=0.1197]
Conduction velocity: 0.6001 m/s [gi=0.1527, ge=0.5486, gm=0.1195]
where gi, ge, and gm are 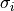 ,
, 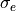 , and
, and 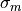 , respectively.
The
, respectively.
The 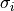 and :math:`{sigma_e}`pair will yield a CV of 0.6 m/s in both monodomain and bidomain simulations.
and :math:`{sigma_e}`pair will yield a CV of 0.6 m/s in both monodomain and bidomain simulations.
Now, for the transverse direction, run
./run.py --velocity 0.3 --converge 1
You should get an output close to the following:
Conduction velocity: 0.6398 m/s [gi=0.1740, ge=0.6250, gm=0.1361]
Conduction velocity: 0.3070 m/s [gi=0.0383, ge=0.1374, gm=0.0299]
Conduction velocity: 0.3001 m/s [gi=0.0365, ge=0.1312, gm=0.0286]
Conduction velocity: 0.3000 m/s [gi=0.0365, ge=0.1311, gm=0.0285]
In this case, the 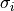 and :math:`{sigma_e}`pair will yield a CV of 0.3 m/s.
and :math:`{sigma_e}`pair will yield a CV of 0.3 m/s.
3D:
Similarly, to run a 3D simulation where 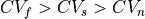 , that is, an orthotropic setup, three sets of conductivities must be defined,
one for each axis
, that is, an orthotropic setup, three sets of conductivities must be defined,
one for each axis 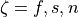 . To compute the set of conductivities for the sheet normal direction,
. To compute the set of conductivities for the sheet normal direction, 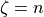 , call the example once
more with
, call the example once
more with 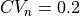
./run.py --velocity 0.2 --converge 1
You should get an output close to the following:
Conduction velocity: 0.6398 m/s [gi=0.1740, ge=0.6250, gm=0.1361]
Conduction velocity: 0.2038 m/s [gi=0.0170, ge=0.0611, gm=0.0133]
Conduction velocity: 0.1998 m/s [gi=0.0164, ge=0.0588, gm=0.0128]
Conduction velocity: 0.2000 m/s [gi=0.0164, ge=0.0590, gm=0.0128]
In this case, the 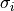 and
and 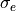 pair will yield a CV of 0.2 m/s.
pair will yield a CV of 0.2 m/s.
Note
Notice that for 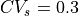 and
and 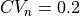 , four iterations were required to converge to
the desired CV, whereas
, four iterations were required to converge to
the desired CV, whereas 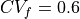 required three. This is because, in this example, the initial conductivity
required three. This is because, in this example, the initial conductivity 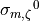 (see Figure Fig. 63) yields a velocity close to 0.6 m/s and is the same in all cases.
Thus, the initial error in CV is larger for
(see Figure Fig. 63) yields a velocity close to 0.6 m/s and is the same in all cases.
Thus, the initial error in CV is larger for 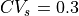 and
and 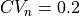 than for
than for 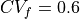 .
.
Tuning Anisotropy Ratios
Defining anisotropy ratios
According to experimental measurements, the intracellular domain is more anisotropic than the extracellular domain, that is, the ratio between the longitudinal and transverse conductivities is larger in the intracellular space than in the extracellular space.
In the intracellular domain, the anisotropy ratio between the longitudinal, 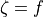 ,
and transverse,
,
and transverse, 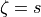 , directions is defined as
, directions is defined as
(35)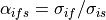
where 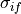 and
and 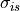 are the intracellular conductivities in the
longitudinal and transverse direction, respectively.
are the intracellular conductivities in the
longitudinal and transverse direction, respectively.
Similarly, in the extracellular domain, the anisotropy ratio between the longitudinal, 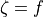 ,
and transverse,
,
and transverse, 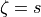 , directions is defined as
, directions is defined as
(36)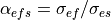
where 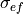 and
and 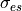 are the extracellular conductivities in the
longitudinal and transverse direction, respectively.
are the extracellular conductivities in the
longitudinal and transverse direction, respectively.
Now, we can express the anisotropy ratio between the two domains as in the longitudinal and transverse directions as
(37)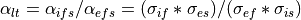
Computing conductivities with a fixed anisotropy ratio
There are many ways to enforce anisotropy ratios between conductivity values. In this tutorial, we use a fixed anisotropy strategy, where, given a anisotropy ratio, we compute a initial transverse conductivity for extracellular domain. The intracellular conductivities as well as the longitudinal extracellular conductivity is kept fixed at default values. Using Equation (37) we obtain:
(38)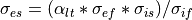
We then tune the longitudinal and transverse conductivities separately using the Iterative scheme. In this manner, we enforce both the desired CV and anisotropy ratio.
The effect of equal and unequal anisotropy ratios
If 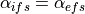 , then
, then 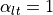 . In this case, the two domains
have equal anisotropy ratios. On the other hand, if
. In this case, the two domains
have equal anisotropy ratios. On the other hand, if 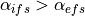 ,
then
,
then 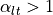 . In this case, the two domains have unequal anisotropy ratios.
unequal anisotropy ratios can only be represented with the bidomain model [2].
. In this case, the two domains have unequal anisotropy ratios.
unequal anisotropy ratios can only be represented with the bidomain model [2].
While anisotropy ratios are of rather minor relevance when simulating impulse propagation in tissue [1], they play a prominent role when the stimulation of cardiac tissue via externally applied electric fields is studied In this case, virtual electrodes appear around the stimulus site, as show in the figure below.
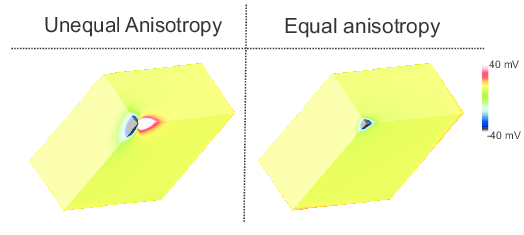
Fig. 69 Induced virtual electrodes in response to a strong hyperpolarizing extracellular stimulus for the equal and unequal anisotropy ratios.
Run anisotropy ratio examples
To compute longitudinal and transverse conductivities for the case of equal anisotropy ratios and 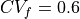 and
and 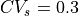 , run
, run
./run.py --ar=1.0
You should get conductivities similar to these:
g_if: 0.152700 g_is: 0.036500 g_ef: 0.548500 g_es: 0.131100
To compute longitudinal and transverse conductivities for the case of unequal anisotropy ratios and 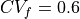 and
and 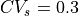 , run
, run
./run.py --ar=3.0
You should get conductivities similar to these:
g_if: 0.152700 g_is: 0.031200 g_ef: 0.548500 g_es: 0.336100
References
| [1] | (1, 2, 3, 4) Costa CM, Hoetzl E, Rocha BM, Prassl AJ, Plank G., Automatic Parameterization Strategy for Cardiac Electrophysiology Simulations, Comput Cardiol 40:373-376, 2013. [Pubmed] |
| [2] | B. J. Caldwell, M. L. Trew, G. B. Sands, D. A. Hooks, I. J. LeGrice, B. H. Smaill, Three distinct directions of intramural activation reveal nonuniform side-to-side electrical coupling of ventricular myocytes., Circ Arrhythm Electrophysiol, vol. 2, no. 4, pp. 433-440, Aug 2009. [Pubmed] |