Constitutive Fitting
Module: tutorials.04_EM_tissue.07_constitutive_fitting.run
Section author: Laura Marx <laura.marx@medunigraz.at>
Fitting of a passive mechanical material model to the Klotz end-diastolic pressure-volume relation (EDPVR).
Klotz Relation
As clinical data of the EDPVR is limited the computational method proposed by [Klotz2007] is used, which enables prediction of the EDPVR by a single measured volume-pressure pair.
According to Klotz et al. the stress-free volume 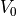 of the left ventricle (LV) can be determined empirically by
of the left ventricle (LV) can be determined empirically by
(56)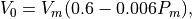
where 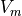 and
and 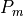 is a measured volume-pressure pair at end diastole.
Further, they showed that the EDPVR can be described by the following power law
is a measured volume-pressure pair at end diastole.
Further, they showed that the EDPVR can be described by the following power law
(57)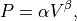
where 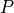 is cavity pressure in mmHg,
is cavity pressure in mmHg, 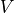 is cavity volume in ml, and the constants
is cavity volume in ml, and the constants 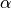 and
and
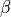 can be defined by the relations
can be defined by the relations
(58)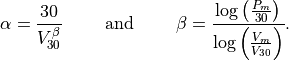
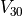 is the cavity volume at a pressure of 30 mmHg, given by
is the cavity volume at a pressure of 30 mmHg, given by
(59)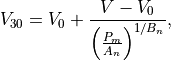
where 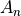 and
and 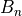 were determined empirically as 27.78 mmHg and 2.76 respectively.
were determined empirically as 27.78 mmHg and 2.76 respectively.
To avoid a singularity in equation (58) 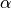 and
and 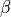 were reposed to
were reposed to
(60)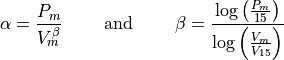
for 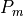 greater than 22 mmHg.
greater than 22 mmHg. 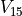 is determined analytically as
is determined analytically as
(61)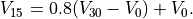
Constitutive Model
As the myocardium is treated as nearly incompressible the strain energy function 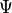 ,
see equation (62), is split into its decoupled form consisting of
a volumetric
,
see equation (62), is split into its decoupled form consisting of
a volumetric 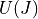 (volume changing) and isochoric part
(volume changing) and isochoric part 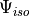 (volume preserving).
(volume preserving).
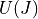 is composed of the bulk modulus
is composed of the bulk modulus  and a penalty term related to the Jacobian J,
see equation (63). Thus, volume change can be penalized and compressibility can be controlled.
and a penalty term related to the Jacobian J,
see equation (63). Thus, volume change can be penalized and compressibility can be controlled.
(62)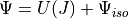
(63)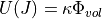
The isochoric strain-energy function is composed of the transversely isotropic constitutive model of Guccione et al. [Guccione1991] consisting of four material parameters, see equation (64).
(64)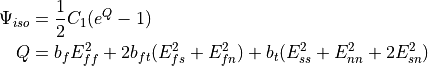
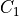 ,
, 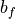 ,
, 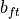 and
and 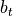 are material parameters accounting for the different
mechanical behavior of the tissue along the fibres (f), across the transverse planes (t) and the fibre-transverse shear
planes.
are material parameters accounting for the different
mechanical behavior of the tissue along the fibres (f), across the transverse planes (t) and the fibre-transverse shear
planes. 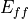 ,
, 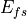 ,
, 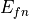 ,
, 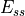 ,
, 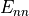 and
and 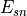 are
projections of the Green-Lagrange strain tensor in fibre (f), sheet(s) and sheet normal (n) direction.
are
projections of the Green-Lagrange strain tensor in fibre (f), sheet(s) and sheet normal (n) direction.
Fitting
Fitting is done by matching cavity volume of the LV in the stress free configuration, approximated during unloading,
and EDPVR with those of the Klotz relation (see Fig. 142).  is set to 650 and
for the material parameters
is set to 650 and
for the material parameters 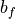 ,
, 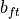 and
and 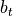 the default values 1.627, 3.580 and 18.480
found by [Guccione1991] are used respectively. The parameter C is then varied to achieve the best fit to the Klotz
Relation.
the default values 1.627, 3.580 and 18.480
found by [Guccione1991] are used respectively. The parameter C is then varied to achieve the best fit to the Klotz
Relation.
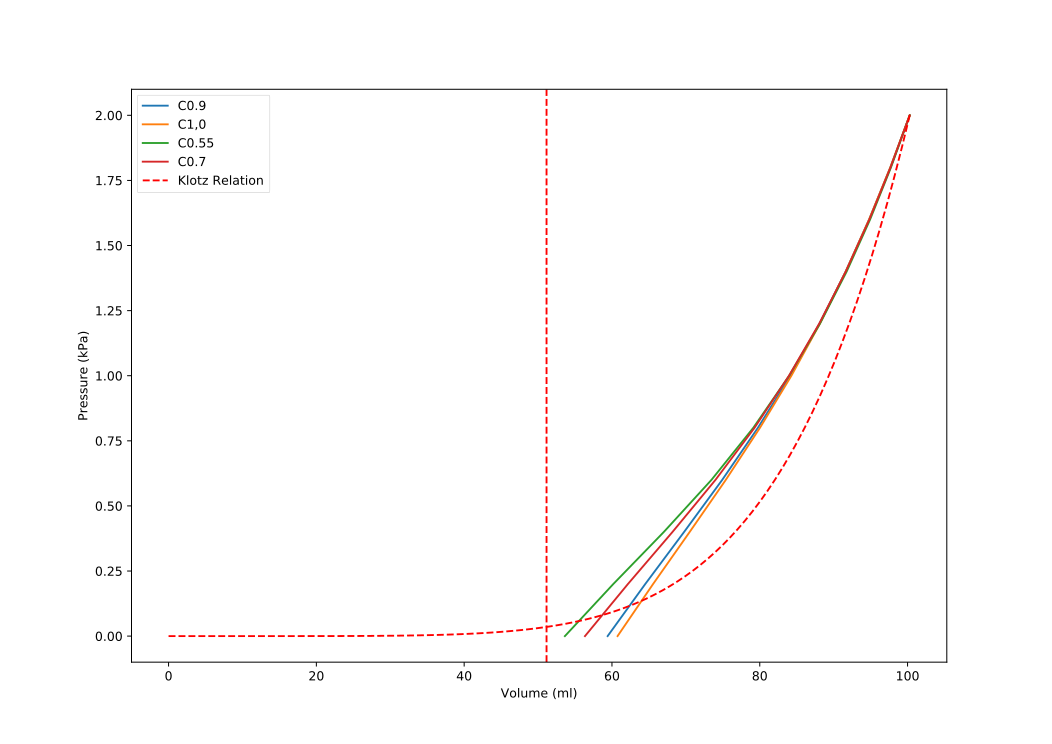
Fig. 142 Klotz end-diastolic pressure-volume relation (EDPVR) (red dashed) and fitted EDPVR with varying paramter C (blue, yellow, green, red)
Example for passive inflation and cavity plot
A simple ring model, assumed to be in stress free configuration, is passively inflated by running the following command in the directory tutorial/inflate:
./run.py --meshtype ring --pressure 2.0 --fast
where meshtype indicates the type of mesh chosen, pressure the maximum pressure to inflate to in kPa and fast sets the resolution and material to fast-solving values.
Switching to the generated file, containing the data files endo.nbc_p.dat and endo.vol.dat with obtained pressure and volume traces, and calling
cavplot endo.nbc_p.dat endo.vol.dat --klotz --pvloop
generates a plot (see Fig. 143) containing the Klotz EDPVR (klotz) and the pressure-volume trace from the data files (pvloop).
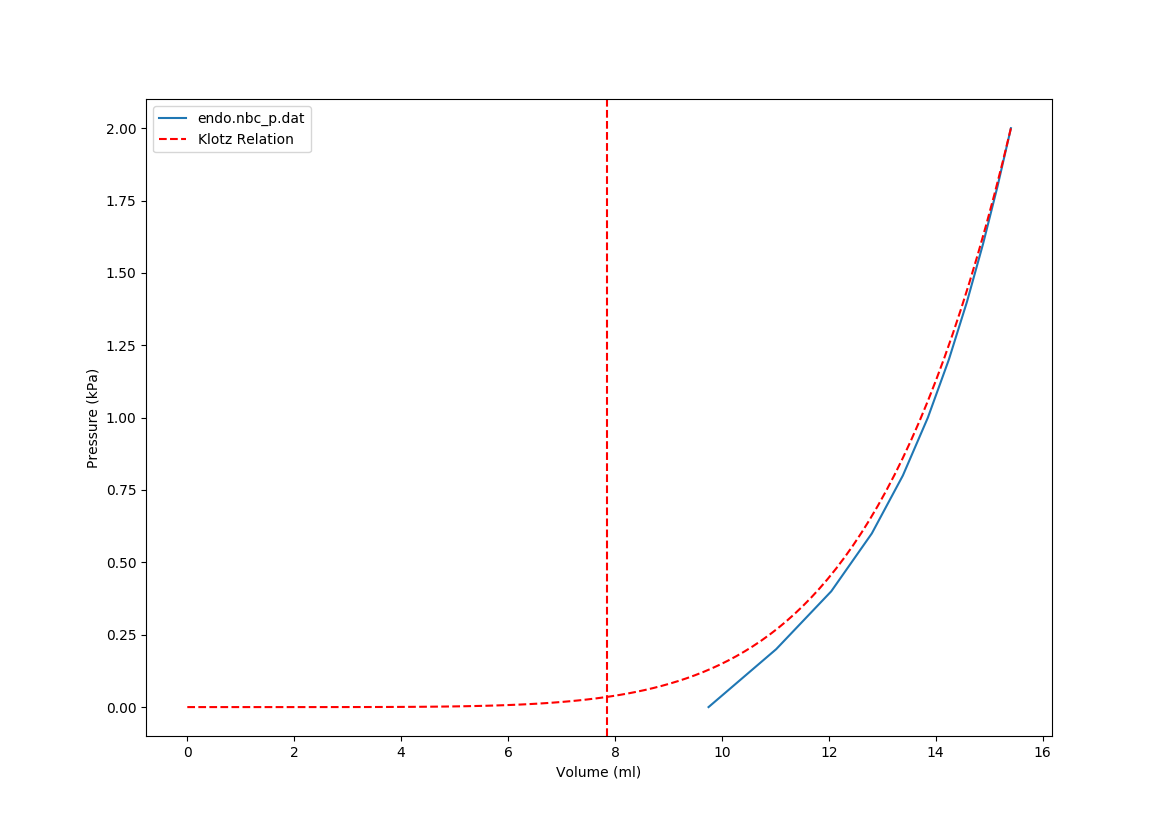
Fig. 143 Klotz end-diastolic pressure-volume relation (EDPVR) (red dashed) and pressure-volume trace recorded during passive inflation (blue).
References
| [Klotz2007] | Klotz, S. and Dickstein, M.L. and Burkhoff, D., A computational method of prediction of the end-diastolic pressure-volume relationship by single beat (2007), Nature Protocols, Volume 2 |
| [Guccione1991] | (1, 2) Guccione, J.L. and McCulloch, A.D. and Waldman, L.K., Passive material properties of intact ventricular myocardium determined from a cylindrical model (1991), J Biomech Eng, Volume 113 |