Preamble
Models of cardiac electromechanics (EM) comprise an electrophysiological and a mechanical component. Electrophysiology is represented by the bidomain equation or simplified derivations and mechanical deformation is described by Cauchy’s equation of motion. In the most general case the two PDE’s are coupled through excitation-contraction coupling (ECC) to translate electrophysiological activity into the buildup of active mechanical stresses, and mechano-electric feedback (MEF) by which the electrophysiological state of the tissue is altered by deformation. The full coupled system is given then by the bidomain equation in its deformed configuation
(30)![\begin{align}
%
\operatorname{Div}\left[J\mathbf{F}^{-1} \left( \boldsymbol{\sigma}_{\mathrm{i}} + \boldsymbol{\sigma}_{\mathrm{e}} \right) \mathbf{F}^{-\top}\nabla\, \phi_{\mathrm{e}}\right]
&= -\operatorname{Div}\left[J \mathbf{F}^{-1} \boldsymbol{\sigma}_{\mathrm{i}} \, \mathbf{F}^{-\top}\nabla V_{\mathrm{m}}\right] -I_{\rm e} \nonumber \\
%
\operatorname{Div}\left[J\mathbf{F}^{-1} \boldsymbol{\sigma}_{\mathrm{i}} \, \mathbf{F}^{-\top} \nabla V_{\mathrm{m}}\right]&=
-\operatorname{Div}\left[J\mathbf{F}^{-1} \boldsymbol{\sigma}_{\mathrm{i}} \, \mathbf{F}^{-\top}\nabla\phi_{\mathrm{e}} \right]
+ \beta \left( I_{\mathrm{m}} - I_{\mathrm{tr}} \right), \nonumber \\
I_m &= C_m \frac{\partial V_m}{\partial t} + I_{\text{ion}}(V_m,\boldsymbol{\eta}_{\rm e},\lambda) \nonumber \\
V_m &= \Phi_i - \Phi_e \nonumber \\
\frac{\partial \boldsymbol{\eta}_{\rm e}} {\partial t} &= f(V_{\rm m}, \boldsymbol{\eta}_{\rm e}, [Ca^{2+}]_{\rm i}(\lambda),\lambda), \nonumber
\end{align}](../_images/math/33ac68487322cd8c7e29f4e3322e00d31df1c8f4.png)
and Cauchy’s equation of motion cast in the so-called Lagrange configuration given as
(31)![\begin{eqnarray}
-\operatorname{Div}\left[ \mathbf{F}\mathbf{S}(\mathbf{u})\right] &=& \mathbf{b}_0
\quad \mbox{ in} \quad \Omega_0 \nonumber \\
\mathbf{S} &=& \mathbf{S}_\mathrm{p}+ \mathbf{S}_\mathrm{a} \nonumber \\
\mathbf{S}_{\mathrm{p}} &=& 2 \frac{\partial \Psi(\mathbf{C})}{\partial \mathbf{C}} \nonumber \\
\mathbf{S}_{\mathrm{a}} &=& \sigma_{\rm a}\left(\mathbf{f}_0^\top\mathbf{C}\mathbf{f}_0\right)^{-1}\mathbf{f}_0 \otimes \mathbf{f}_0 \nonumber \\
\sigma_{\rm a} &=& f(\boldsymbol{\eta}_{\rm m}, [Ca^{2+}]_{\rm i}, [Ca^{2+}]_{\rm TnC}, \lambda,\dot{\lambda}) \nonumber \\
\lambda &=& \sqrt{\mathbf{f}_0^\top \mathbf{C} \mathbf{f}_0} \nonumber \\
\mathbf{u}&=&\mathbf{u}_{\mathrm{D},0}\quad\mbox{ on } \Gamma_{\mathrm{D},0} \nonumber \\
\mathbf{F}\mathbf{S}\mathbf{n}_0&=&-p J {\bf F}^{-\top}\mathbf{n}_0\quad\mbox{ on } \Gamma_{\mathrm{N},0} \nonumber
\end{eqnarray}](../_images/math/96cc09f70ba35b7eaa4144996eef16ac6783ebed.png)
The physiology of EP is coupled to deformation through excitation-contraction coupling (ECC). During an action potential Calcium is released from intracellular stores inducing a rise in intracellular Calcium concentration
EP is influenced by deformation as well through mechano-electric feedback (MEF).
This is mainly driven by length-dependence of Calcium binding and stretch-activated sacrolemnal currents,
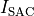 , which modulated their conductivity as a function of fiber stretch,
, which modulated their conductivity as a function of fiber stretch, 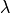 .
.
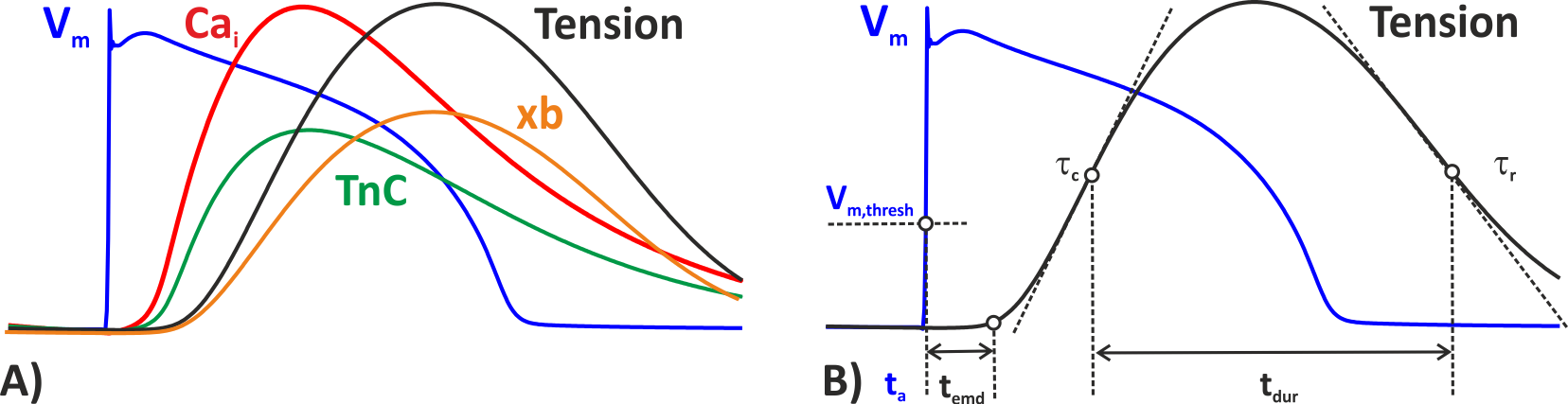
Fig. 52 ECC mechanisms as implemented in carpentry. A) Physiological Calcium-based coupling mechanism: The upstroke of the action potential
triggers Calcium release from intracellular Calcium stores, thus driving the Calcium concentration up in the cytosol.
Calcium binds to Troponin C and mediates the formation of force-generating cross-bridges, xb, in myofilaments,
that leads then to the buildup of mechanical forces shortening the myocyte. Calcium is being pumped back into the intracellular stores
through the SERCA pump or removed from the cell through the sodium-Calcium exchanger current, 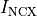 .
B) Phenomenological active stress models are triggered based on a prescribed activation time. In carpentry
the instant of triggering is derived from the upstroke of the AP after a given delay,
.
B) Phenomenological active stress models are triggered based on a prescribed activation time. In carpentry
the instant of triggering is derived from the upstroke of the AP after a given delay,  ,
the electro-mechanical delay (which is fixed in this case and not a function of activation time as it would be in the physiological
case). The shape of the phenomenological tension transient can be matched to fit experimental measurements,
by adjusting parameters such as the rate of contraction,
,
the electro-mechanical delay (which is fixed in this case and not a function of activation time as it would be in the physiological
case). The shape of the phenomenological tension transient can be matched to fit experimental measurements,
by adjusting parameters such as the rate of contraction, 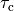 or relaxation,
or relaxation, 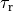 ,
the peak tension developed and the duration of the force twitch,
,
the peak tension developed and the duration of the force twitch, 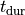 .
.