`Electrical Flow Field`

Module: devtests.bidomain.electric_flow_field.run

Section author: Anton Prassl <anton.prassl@medunigraz.at> and Gernot Plank <gernot.plank@medunigraz.at>

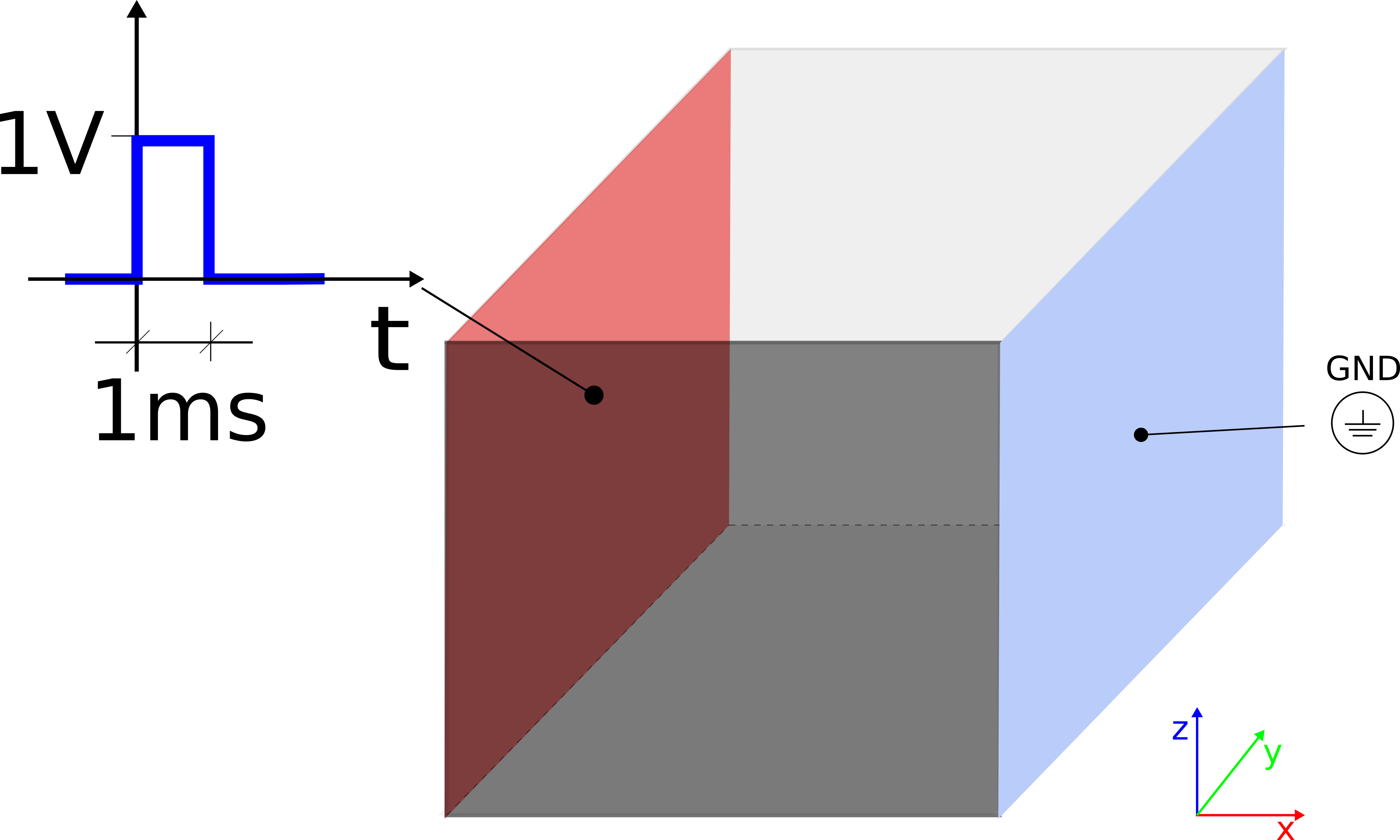
Fig. 13 Experimental setup to validate the electrical flow field.

Initial Conditions

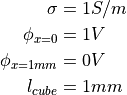
$\sigma &= 1 S/m \\ \phi_{x=0} &= 1V \\ \phi_{x=1mm} &= 0V \\ l_{cube} &= 1mm$

Electric Conductivity and Resistance

$Conductivity\, G &= \sigma \cdot \frac{A}{l} = 1[\frac{S}{m}] \cdot \frac{1[mm^2]}{1[mm]} = 1\left[ \frac{S}{m} \right] \cdot 1[mm] = 1mS\\ Resistance\, R &= \frac{1}{G} = 1 k\Omega$

Electric Field E

$E_x &= \frac{1[V]}{1[mm]} \vec{e_x} = \frac{1000[mV]}{10^3[\mu m]} \vec{e_x} = 1\left[ \frac{mV}{\mu m}\right] \vec{e_x} \\ \vec{E} &= \begin{bmatrix} 1 \\ 0 \\ 0 \end{bmatrix} \left[\frac{mV}{\mu m} \right] \\$

Electric Current Density J

$\vec{J} &= \begin{bmatrix} \sigma\, 0\, 0 \\ 0\, \sigma\, 0\\ 0\, 0\, \sigma \end{bmatrix} \begin{bmatrix} E_x \\ E_y \\ E_z \end{bmatrix} = \begin{bmatrix} E_x \\ 0\\ 0 \end{bmatrix} \left[\frac{S}{m} \cdot \frac{mV}{\mu m} \right] \\ J_x &= 1 \left[ \frac{S}{m} \right] \cdot 1 \left[ \frac{mV}{\mu m} \right] = 1 \left[ \frac{10^3 mS}{10^6 \mu m} \right] \cdot 1 \left[ \frac{mV}{\mu m} \right] = 10^{-3} \left[ \frac{\mu A}{\mu m^2} \right]$

Electric Current

$I = U \cdot G = 1[V] \cdot 1[mS] = 1 mA$

Electric Power P

$P = U \cdot I = 1[V] \cdot 1[mA] = 1 mW$

Electric Power Density

$Power Density = P / V = \frac{1 [mW]}{1 [mm^3]} = 1 \left[ \frac{mW}{mm^3} \right]$

Tests

serial

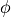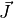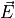Solve Laplace’s equation on a 1mm cube and compare $\phi$ , $\vec{J}$ and $\vec{E}$ against reference.

Tags: FAST SERIAL

Checks:

Compare against stored reference: max_error(phie.igb)
Compare against stored reference: max_error(PostProcess/E_field.igb)
Compare against stored reference: max_error(PostProcess/J_field.igb)

Last run: 2024-02-29 00:12:10.865754, revision {‘base’: ‘cbf8efd0’}, dependency revisions {PT_C: 31642c1e,cvsys: 593686bc,eikonal: 5fbbfda3,elasticity: 4d92ddfc}

Runtime: 0:00:00.605489
ALL PASSED
  PASS max_error(phie.igb): 0.0
  PASS max_error(PostProcess/E_field.igb): 0.0
  PASS max_error(PostProcess/J_field.igb): 0.0

parallel

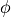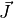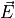Solve Laplace’s equation on a 1mm cube and compare $\phi$ , $\vec{J}$ and $\vec{E}$ against reference.

Tags: FAST PARALLEL

Checks:

Compare against stored reference: max_error(phie.igb)
Compare against stored reference: max_error(PostProcess/E_field.igb)
Compare against stored reference: max_error(PostProcess/J_field.igb)

Last run: 2024-02-29 00:12:11.509337, revision {‘base’: ‘cbf8efd0’}, dependency revisions {PT_C: 31642c1e,cvsys: 593686bc,eikonal: 5fbbfda3,elasticity: 4d92ddfc}

Runtime: 0:00:00.515709
ALL PASSED
  PASS max_error(phie.igb): 0.0
  PASS max_error(PostProcess/E_field.igb): 0.0
  PASS max_error(PostProcess/J_field.igb): 0.0