Single Cell Scale
For electrophysiological simulation, the basic unit of the model is the cellular activity. Cellular models of cardiac electrical activity were first constructed over 50 years ago, and today, these models have been refined and are routinely put into organ scale simulations. The modelling components are described below.
Ionic models refer to the electrical representation of the cell based on the movement of ions across the cell membrane, resulting in a change in the voltage across the membrane. Schematically, a capacitor is placed in parallel with a number of ionic transport mechanisms. In general, an ionic model is of the form
(1)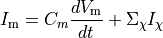
where 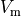 is the voltage across the cell membrane,
is the voltage across the cell membrane,
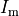 is the net current across the membrane,
is the net current across the membrane,
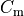 is the membrane capacitance,
and
is the membrane capacitance,
and 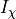 is a particular transport mechanism, either a channel, pump or exchanger.
Additional equations may track ionic concentrations and the processes which affect them,
like calcium-induced release from the sarcoplasmic reticulum.
By convention, outward current, i.e., positive ions leaving the cell, is defined as being positive, while inward currents are negative.
is a particular transport mechanism, either a channel, pump or exchanger.
Additional equations may track ionic concentrations and the processes which affect them,
like calcium-induced release from the sarcoplasmic reticulum.
By convention, outward current, i.e., positive ions leaving the cell, is defined as being positive, while inward currents are negative.
Channels are represented as resistors in series with a battery. The battery represents the Nernst Potential resulting from the electrical field developed by the ion concentration difference across the membrane. It is given by
(2)![\begin{equation}
E_S = \frac{RT}{zF}\ln\frac{[S]_i}{[S]_e} \nonumber
\end{equation}](../_images/math/4dafc5d04367cbc739a36281b672218e1392c089.png)
where 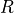 is the gas constant,
is the gas constant,
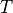 is the temperature,
is the temperature,
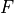 is Faraday’s constant and
is Faraday’s constant and  is the valence of the ion species
is the valence of the ion species 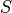 .
Channels are dynamical systems which open and close in response to various conditions
like transmembrane voltage, stretch, ligands, and other factors.
The opening and closing rates of the channels vary by several orders of magnitudes, and are generally, nonlinear in nature.
Thus, the equivalent electrical resistance of a channel is a time dependent quantity.
.
Channels are dynamical systems which open and close in response to various conditions
like transmembrane voltage, stretch, ligands, and other factors.
The opening and closing rates of the channels vary by several orders of magnitudes, and are generally, nonlinear in nature.
Thus, the equivalent electrical resistance of a channel is a time dependent quantity.
The first representation of a cardiac cell was that produced by D. Noble of a Purkinje cell, based on modification of the Hodgkin-Huxley nerve action potential. Since then, hundreds of models have been developed for many reasons. Ionic models need to be developed to match experimental procedures if the models are to be predictive and offer insight into mechanistic workings. In mammals, action potential durations range from tens of milliseconds for mice to several hundreds of milliseconds for large animals. Atrial myocyte protein expression is quite different from that of ventricular myocytes, resulting in different action potential durations and shapes. Even nearby cells exhibit action potential differences due to slightly different levels of channel protein expression. The complexity of ionic models has been steadily growing as more knowledge is gained through better experimental techniques, equipment and specific blockers of transport mechanisms. As more mechanisms are identified as affecting electrophysiology, either directly or indirectly, they are incorporated into ionic models. Selection of the model to use is not always obvious as different models may be available for the same species and heart location, which may yield quite different behaviour. Regardless, identifying the strengths and weaknesses of an ionic model for a particular application is important.
Ionic models may be biophysically detailed or phenomenological. Biophysically detailed models attempt to discretely depict important currents and processes within the cell. Early models had approximately ten equations depicting only sodium and potassium channels, while present models have hundreds of equations taking into account not only membrane ion transporters, but intracellular calcium handling, mitochondrial function, and biochemical signalling pathways. Conversely, phenomenological ionic models use a set of currents which faithfully reproduce whole cell behaviour in terms of action potential shape and duration, and restitution properties. The currents in the phenomenological model are not physiological but can be considered as amalgamations of known currents. While these models are computationally much simpler and easier to tune, they lose the direct correspondence with the biophysics which makes implementing drug effects or cellular pathologies challenging. Finally, cellular automata models have also been used, and can be considered as a type of phenomenological model. These models do not use differential equations but have a set of rules which dictate transitions between discrete states of the model. As such, these models are computationally light, and can be as detailed as required. However, behaviour may not be as rich as differential equations. The choice of model, biophysical or phenomenological, depends on the nature of the problem being considered, and the availability of computational resources for the problem size.
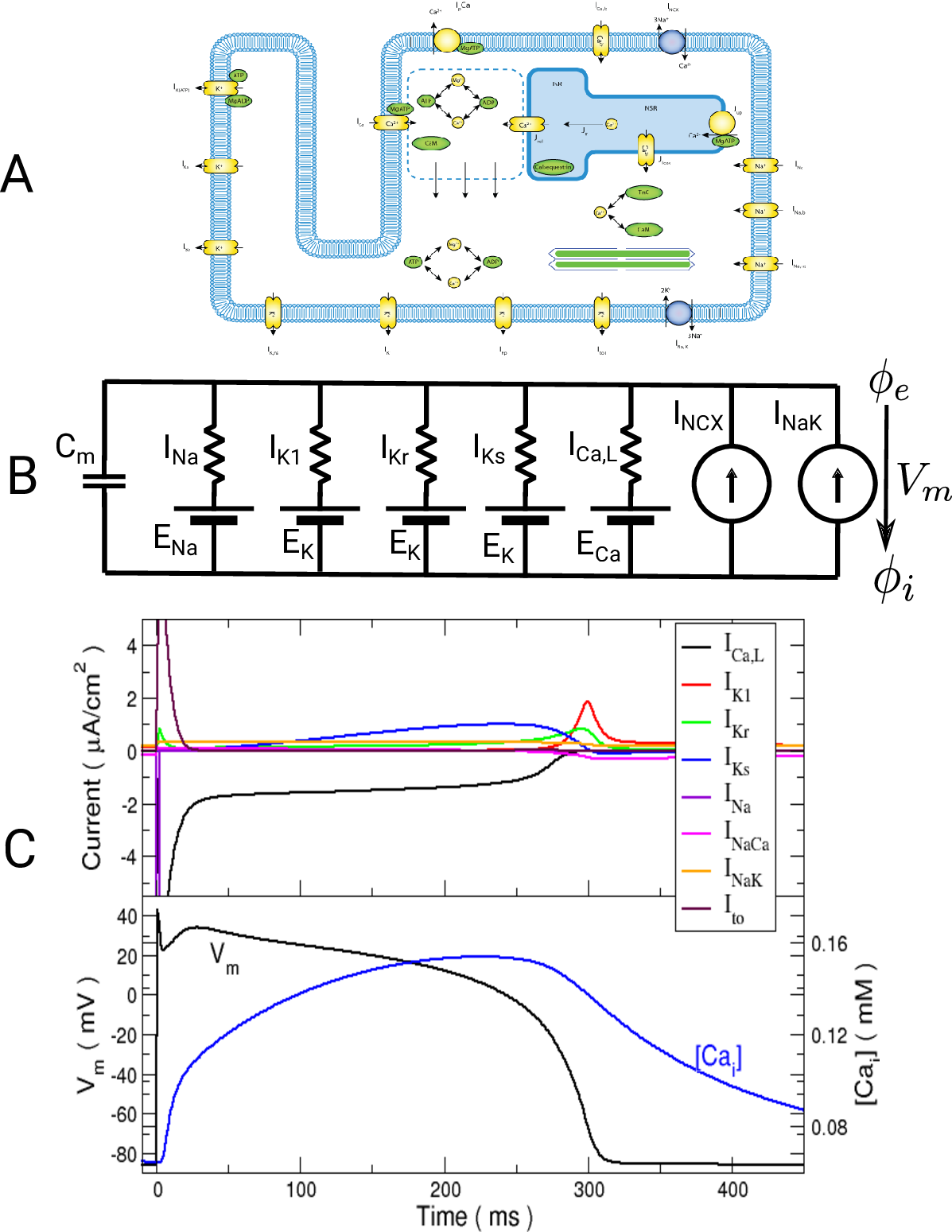
Fig. 34 Ionic models A: Myocyte schematic showing the membrane (blue) which contains channels (yellow cylinders),
pumps (yellow circles) and exchangers (blue circles).
The sarcoplasmic reticulum is divided into the junctional (JSR) and network (NSR) regions
and channels and pumps control ion movement into and out of it.
Figure taken from
Michailova et al.
B: Electrical representation of a cell showing a limited number of currents:
fast sodium (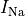 ),
inward rectifier (
),
inward rectifier (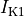 ),
fast and slow repolarizing currents (
),
fast and slow repolarizing currents (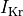 and
and 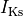 )
L-type calcium (
)
L-type calcium (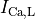 },
the sodium-potassium pump (
},
the sodium-potassium pump (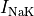 ) and the sodium-calcium exchanger (
) and the sodium-calcium exchanger (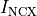 ).
Nernst potentials for the ionic species are indicated (
).
Nernst potentials for the ionic species are indicated (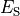 ) as is the membrane capacitance (
) as is the membrane capacitance (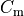 ).
C: Effect of applying a suprathreshold current at time 0 to the ten Tuscher ionic model of the human ventricular myocyte.
Top: Major ionic currents. Note that the following currents are clipped:
).
C: Effect of applying a suprathreshold current at time 0 to the ten Tuscher ionic model of the human ventricular myocyte.
Top: Major ionic currents. Note that the following currents are clipped:
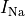 (-46.4),
(-46.4), 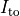 (15.3), and
(15.3), and 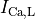 (-9.6).
Bottom: the resulting action potential (
(-9.6).
Bottom: the resulting action potential (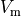 ) and myoplasmic calcium transient (
) and myoplasmic calcium transient (![[Ca_{\rm i}]](../_images/math/de0023b1b167317826d96b7479be82cbf11eeb2b.png) ). }
). }
When considering the mathematical description of ionic channels, there are two main approaches which are detailed below.
Hodgkin-Huxley Dynamics
The Hodgkin-Huxley approach is named after the Nobel laureates
who were the first to develop a mathematical model of the neural action potential.
Single channel activity recordings show that channels have a small set of discrete conductance states, with
the channel stochastically transitioning between closed states and open states.
Short time analysis of a single channel is very difficult to interpret
but ensemble averaging clearly reveals smooth kinetics in changes of channel conductance.
In the Hodgkin-Huxley formulation, channel conductance
is assumed to be controlled by gates which take on values between 0 and unity, representing the portion of the cells in one state.
Since cells have hundreds of ion channels if not more, this approximation holds well.
Current flow produced by ion species 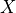 passing through a channel is then described by
passing through a channel is then described by
(3)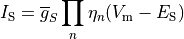
where 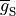 is the maximum conductance of the channel and
is the maximum conductance of the channel and 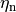 is a gating variable.
Often the gating variable is assumed to follow first order dynamics so
is a gating variable.
Often the gating variable is assumed to follow first order dynamics so
(4)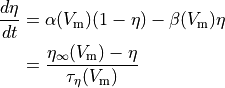
where 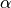 and
and 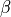 are rates
which can be cast into an equivalent form of a steady state value (
are rates
which can be cast into an equivalent form of a steady state value (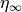 )
and a rate of change (
)
and a rate of change (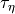 ).
The advantage of this latter formulation is that mathematically,
the update of the gating variables can be performed by a numercial integration method,
the Rush-Larsen technique, which is guaranteed to unconditionally keep the gating variable bounded
within the range [0,1] while allowing a large time step.
).
The advantage of this latter formulation is that mathematically,
the update of the gating variables can be performed by a numercial integration method,
the Rush-Larsen technique, which is guaranteed to unconditionally keep the gating variable bounded
within the range [0,1] while allowing a large time step.
Markov Models
Markov models describe the channel as a set off states, such as the conductance states seen in single channel recordings, as well as the non conducting states through which a channel must pass to reach them. Transitions between states are described by rate constants which can be functions of concentrations or voltages, or fixed. These is a variables for each state which represent the portion of channels in a cell which are in that state. As such, the sum of state variables is unity. A Hodgkin-Huxley made can be converted to a Markov model by considering a gating variable as a two state model. However, the advantage of the Markov representation is its ability to model drug interaction. Essentially, drug binding doubles the number of possible states in an ionic model, augmenting the original states with drug-bound versions. One may easily limit drug binding to a particular subset of channel states, and more finely control channel kinetics.
bench - Single Cell Modeling Tool
The single cell experimentation tool bench is quite versatile and can be used
to replicate a wider range of single cell experimental protocols.
A tutorial on how to use bench is given here.
The following sections demonstrate how one explores all available
bench functions and explains the command line arguments available.
Getting Help
The --help, --detailed-help or --full-help arguments provide a list of all available arguments
with increasing levels of detail.
bench --help
LIMPET 1.1
Use the IMP library for single cell experiments. All times in ms; all voltages
in mV; currents in uA/cm^2
Usage: LIMPET [-h|--help] [--detailed-help] [--full-help] [-V|--version]
[-cFLOAT|--stim-curr=FLOAT] [--stim-volt=FLOAT] [--stim-file=STRING]
[-aDOUBLE|--duration=DOUBLE] [-DDOUBLE|--dt=DOUBLE] [-nINT|--num=INT]
[--ext-vm-update] [--rseed=INT] [-TDOUBLE|--stim-dur=DOUBLE]
[-A|--stim-assign] [--stim-species=STRING] [--stim-ratios=STRING]
[--resistance=DOUBLE] [-ISTRING|--imp=STRING]
[-pSTRING|--imp-par=STRING] [-PSTRING|--plug-in=STRING]
[-mSTRING|--plug-par=STRING] [--load-module=STRING]
[-lDOUBLE|--clamp=DOUBLE] [-LDOUBLE|--clamp-dur=DOUBLE]
[--clamp-start=DOUBLE] [--clamp-SVs=STRING] [--SV-clamp-files=STRING]
[--SV-I-trigger] [--AP-clamp-file=STRING] [-NDOUBLE|--strain=DOUBLE]
[-tDOUBLE|--strain-time=DOUBLE] [-yFLOAT|--strain-dur=FLOAT]
[--strain-rate=DOUBLE] [-oDOUBLE|--dt-out=DOUBLE]
[-OSTRING|--fout=STRING] [--no-trace] [--trace-no=INT] [-B|--bin]
[-uSTRING|--imp-sv-dump=STRING] [-gSTRING|--plug-sv-dump=STRING]
[-d|--dump-lut] [--APstatistics] [-v|--validate]
[-sDOUBLE|--save-time=DOUBLE] [-fSTRING|--save-file=STRING]
[-rSTRING|--restore=STRING] [-FSTRING|--save-ini-file=STRING]
[-SDOUBLE|--save-ini-time=DOUBLE] [-RSTRING|--read-ini-file=STRING]
[--SV-init=STRING]
or : LIMPET [--list-imps] [--plugin-outputs] [--imp-info]
or : LIMPET [--stim-times=STRING]
or : LIMPET [--numstim=INT] [-iDOUBLE|--stim-start=DOUBLE]
[-bDOUBLE|--bcl=DOUBLE]
or : LIMPET --restitute=STRING [--res-file=STRING] [--res-trace]
or : LIMPET --clamp-ini=DOUBLE --clamp-file=STRING
-h, --help Print help and exit
--detailed-help Print help, including all details and hidden
options, and exit
--full-help Print help, including hidden options, and exit
-V, --version Print version and exit
Mode: regstim
regular periodic stimuli
--numstim=INT number of stimuli (default=`1')
-i, --stim-start=DOUBLE start stimulation (default=`1.')
-b, --bcl=DOUBLE basic cycle length (default=`1000.0')
Mode: neqstim
irregularly timed stimuli
--stim-times=STRING comma separated list of stim times (default=`')
Mode: restitute
restitution curves
--restitute=STRING restitution experiment (possible
values="S1S2", "dyn", "S1S2f")
--res-file=STRING definition file for restitution parameters
(default=`')
--res-trace output ionic model trace (default=off)
Mode: info
output IMP information
--list-imps list all available IMPs (default=off)
--plugin-outputs list the outputs of available plugins
(default=off)
--imp-info print tunable parameters and state variables for
particular IMPs (default=off)
Mode: vclamp
Constant Voltage clamp
--clamp-ini=DOUBLE outside of clamp pulse, clamp Vm to this value
(default=`-80.0')
--clamp-file=STRING clamp voltage to a signal read from a file
(default=`')
Group: stimtype
stimulus type
-c, --stim-curr=FLOAT stimulation current (default=`60.0')
--stim-volt=FLOAT stimulation voltage
--stim-file=STRING use signal from a file for current stim
Simulation control:
-a, --duration=DOUBLE duration of simulation (default=`1000.')
-D, --dt=DOUBLE time step (default=`.01')
-n, --num=INT number of cells (default=`1')
--ext-vm-update update Vm externally (default=off)
--rseed=INT random number seed (default=`1')
Stimuli:
-T, --stim-dur=DOUBLE duration of stimulus pulse (default=`1.')
-A, --stim-assign stimulus current assignment (default=off)
--stim-species=STRING concentrations that should be affected by
stimuli, e.g. 'K_i:Cl_i' (default=`K_i')
--stim-ratios=STRING proportions of stimlus current carried by each
species, e.g. '0.7:0.3' (default=`1.0')
--resistance=DOUBLE coupling resistance [kOhm] (default=`100.0')
Ionic Models:
-I, --imp=STRING IMP to use (default=`MBRDR')
-p, --imp-par=STRING params to modify IMP (default=`')
-P, --plug-in=STRING plugins to use, separate with ':' (default=`')
-m, --plug-par=STRING params to modify plug-ins, separate params with
',' and plugin params with ':' (default=`')
--load-module=STRING load a module for use with bench (implies --imp)
(default=`')
Voltage clamp pulse:
-l, --clamp=DOUBLE clamp Vm to this value (default=`0.0')
-L, --clamp-dur=DOUBLE duration of Vm clamp pulse (default=`0.0')
--clamp-start=DOUBLE start time of Vm clamp pulse (default=`10.0')
Clamps:
--clamp-SVs=STRING colon separated list of state variable to clamp
(default=`')
--SV-clamp-files=STRING : separated list of files from which to read
state variables (default=`')
--SV-I-trigger apply SV clamps at each current stim
(default=on)
--AP-clamp-file=STRING action potential trace applied at each stimulus
(default=`')
Strain:
-N, --strain=DOUBLE amount of strain to apply (default=`0')
-t, --strain-time=DOUBLE time to strain (default=`200')
-y, --strain-dur=FLOAT duration of strain (default=tonic) [ms]
--strain-rate=DOUBLE time to apply/remove strain (default=`2')
Output:
-o, --dt-out=DOUBLE temporal output granularity (default=`1.0')
-O, --fout[=STRING] output to files (default=`BENCH_REG')
--no-trace do not output trace (default=off)
--trace-no=INT number for trace file name (default=`0')
-B, --bin write binary files (default=off)
-u, --imp-sv-dump=STRING sv dump list (default=`')
-g, --plug-sv-dump=STRING : separated sv dump list for plug-ins, lists
separated by semicolon (default=`')
-d, --dump-lut dump lookup tables (default=off)
--APstatistics compute AP statistics (default=off)
-v, --validate output all SVs (default=off)
State saving/restoring:
-s, --save-time=DOUBLE time at which to save state (default=`0')
-f, --save-file=STRING file in which to save state (default=`a.sv')
-r, --restore=STRING restore saved state file (default=`a.sv')
-F, --save-ini-file=STRING text file in which to save state of a single
cell (default=`singlecell.sv')
-S, --save-ini-time=DOUBLE time at which to save single cell state
(default=`0.0')
-R, --read-ini-file=STRING text file from which to read state of a single
cell (default=`singlecell.sv')
--SV-init=STRING colon separated list of comma separated
SV=initial_values
Available models
The --list-imps argument outputs a list of all available ionic models and plugins.
bench --list-imps
Ionic models:
AlievPanfilov
ARPF
Steward
converted_COURTEMANCHE
converted_DiFranNoble
converted_LRDII_F
converted_MBRDR
converted_NYGREN
converted_RNC
converted_TT2
converted_UCLA_RAB
UCLA_RAB_SCR
COURTEMANCHE
DiFranNoble
ECME
FHN_RMcC
FOX
GPB
GPVatria
GPB_Land
GW_CAN
hAMr
HH
IION_SRC
INADA_AVN
Iribe
JBTT2
Kurata
LMCG
LR1
LRDII
LRDII_F
MacCannell_Fb
MitchellSchaeffer
mMS
MBRDR
MurineMouse
NYGREN
ORd
Pandit
PASSIVE
PUG
Rat_neon
RNC
SC
TT2
TT
TTRED
UCLA_RAB
WANG_NNR
SHANNON
GTT2_fast
GTT2_fast_PURK
JB_COURTEMANCHE
Plug-ins:
converted_EP
converted_EP_RS
converted_IA
EP
EP_RS
ExcConNHS
I_ACh
IA
IFun
I_KATP
INa_Bond_Markov
I_NaH
Muscon
NPStress
FxStress
TanhStress
Rice
LandStress
NHSstress
Lumens
SAC_KS
YHuSAC
Show model state variables and exposed parameters
The --imp-info argument lists all state variables of a model
and all exposed parameters which can be modified.
For instance, to interrogate this for the tenTusscher 2 model run:
bench --imp TT2 --imp-info
TT2:
big_cnt 0
fmode 0
Ko 5.4
Cao 2
Nao 140
Vc 0.016404
Vsr 0.001094
Bufc 0.2
Kbufc 0.001
Bufsr 10
Kbufsr 0.3
Vmaxup 0.006375
Kup 0.00025
R 8314.47
F 96485.3
T 310
RTONF 26.7138
CAPACITANCE 0.185
Gkr 0.153
pKNa 0.03
Gks 0.392
GK1 5.405
Gto 0.294
GNa 14.838
GbNa 0.00029
KmK 1
KmNa 40
knak 2.724
GCaL 3.98e-05
GbCa 0.000592
knaca 1000
KmNai 87.5
KmCa 1.38
ksat 0.1
n 0.35
GpCa 0.1238
KpCa 0.0005
GpK 0.0146
scl_tau_f 1
flags ENDO|EPI|MCELL
State variables:
Ca_i
CaSR
CaSS
R_
O
Na_i
K_i
M
H
J
Xr1
Xr2
Xs
R
S
D
F
F2
FCaSS
The --plugin-outputs argument provides the same information as --imp-info,
but lists in addition all the outputs of plugins, that is,
global quantities modified by a given plugins.
Plug-ins:
converted_EP Iion
converted_EP_RS Iion
converted_IA Iion
EP Iion
EP_RS Iion
ExcConNHS Tension
I_ACh Iion
IA Iion
IFun Iion
I_KATP K_e Iion
INa_Bond_Markov Iion
I_NaH Na_e
Muscon Tension
NPStress Tension
FxStress Tension
TanhStress Tension
Rice Tension
LandStress Tension
NHSstress Tension
Lumens delLambda Tension
SAC_KS Iion
YHuSAC Iion
Define a stimulus
The arguments --stim-curr and --stim-volt select the magnitude of a current or voltage stimulus pulse
in 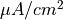 and
and  , respectively.
The duration of a stimulus is set through the
, respectively.
The duration of a stimulus is set through the stim-dur argument.
Alternatively, a trace file can be provided through --stim-file to impose a stimulus of arbitrary shape.
To initiate an action potential in the TT2 model by applying a current stimulus of 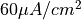 and 2 ms duration run
and 2 ms duration run
bench --stim-curr 60 --stim-dur 2
or, to stimulate with an arbitrary stimulus current profile run
bench --stim-file mypulse.trc
where the stimulus definition file mypulse.trc must comply with the following format:
#samples
t0 y0
t1 y1
t2 y2
...
tN yN
Define a stimulus protocol
Two types of protocols are supported, a train of regular periodic stimuli or a train of irregularly time stimuli.
In the regular case the total number of stimuli to be delivered is prescribed by --numstim
and the interval between stimuli by the basic cycle length argument --bcl.
The stimulus protocol is initiated at a given time prescribed by --stim-start.
bench --imp TT2 --numstim 50 --stim-start 10. --bcl 350
An irregular stimulus sequence is specified through the --stim-times argument.
bench --imp TT2 --stim-times 10,360,700,920
The response to this stimulus definition is illustrated here.
When using the --stim-times options the number of stimuli depends solely on the times provided,
using the --num-stim causes a conflict.
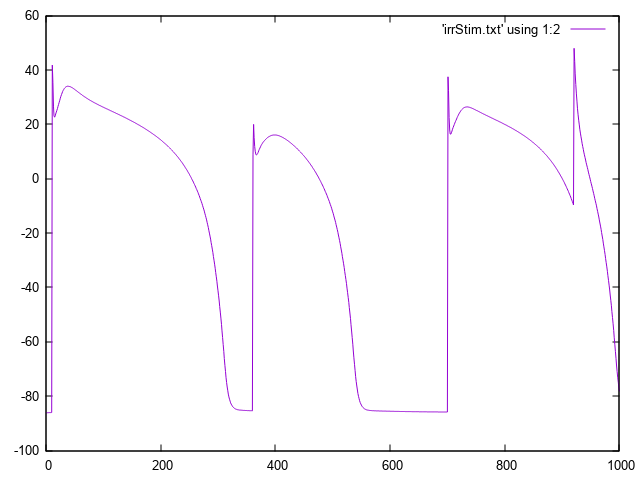
Fig. 35 Irregular basic cycle length due to stimulation using --stim-times.
Read the default command line output
Depending on the ionic model and the plugins used global variables which may diffuse at the tissue level are written to the console. The output will look similar to
bench --imp TT2
Outputting the following quantities at each time:
Time Vm Iion
0.000 -8.62000000e+01 +0.00000000e+00
1.000 -8.61618521e+01 -3.46181728e-02
2.000 +4.10176938e+01 -6.35646133e+01
3.000 +3.51969845e+01 +1.22923870e+01
4.000 +2.62015535e+01 +5.84205961e+00
5.000 +2.29077661e+01 +1.52032351e+00
...
To quickly visualize AP shape or ionic current redirect the output to a file and visualize with your preferred tool.
Basic stimulation control
The overall duration of simulation is set by --duration in [ms] and the integration time step is chosen by --dt in [ms].
The time stepping method cannot be chosen at the command line as ODE integration in LIMPET is hardcoded,
but the source code for any ionic model can be regenerated with a different integration scheme
(see limpet_fe.py for details). To simulate 10 action potentials at a basic cycle length of 500 ms
the overall duration of the simulation should be picked as 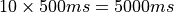 .
.
bench --duration 5000 --bcl 500 --num-stim 10 --stim-start 0
Simple AP visualization
To quickly visualize the shape of an action potential or the ionic current redirect the output to a file
bench --duration 400 --dt-out 0.1 --fout=AP
Time 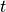 , transmembrane voltage
, transmembrane voltage 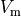 and ionic current,
and ionic current, 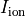 are written to the file
are written to the file AP.txt. Use your favourite plotting tool such as, for instance, gnuplot.
gnuplot
# plot Vm
plot 'AP.txt' using 1:2 with lines
# plot Iion
plot 'AP.txt' using 1:3 with lines
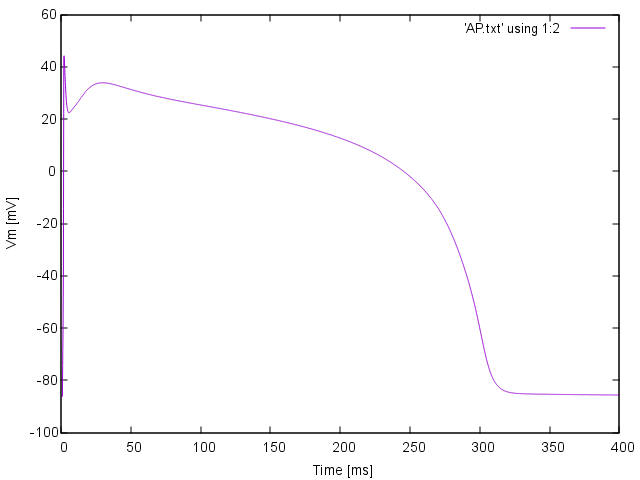
Fig. 36 Simple AP visualization with gnuplot
Performance benchmarking
For the sake of performance benchmarking the number of cell solved can be increased using --num.
Performance metrics of the ODE solver are reported in any simulation run at the end of the output.
To run a short benchmark simulating 10 ms of activity in 10000 cells use:
mpiexec -n 16 bench --num 100000 --duration 10
This outputs a basic performance statistics as shown below:
setup time 0.001208 s
initialization time 0.036891 s
main loop time 2.801997 s
total ode time 2.788086 s
mn/avg/mx loop time 2.064943 2.799198 5.839109 ms
mn/avg/mx ODE time 2.063036 2.785301 5.825996 ms
real time factor 0.003587
Model modification
Model behavior can be modified by providing parameter modification string through --imp-par.
Modifications strings are of the following form:
param[+|-|/|*|=][+|-]###[.[###][e|E[-|+]###][\%]
where param is the name of the parameter one wants to modify
such as, for instance, the peak conductivity of the sodium channel, GNa.
Not all parameters of ionic models are exposed for modification,
but a list of those which are can be retrieved for each model using imp-info.
As an example, let’s assume we are interested in specializing a generic human ventricular myocyte
based on the ten Tusscher-Panfilov model to match the cellular dynamics of myocytes
as they are found in the halo around an infarct, i.e.in the peri-infarct zone (PZ).
In the PZ various current are downregulated.
Patch-clamp studies of cells harvested from the peri-infract zone have reported
a 62% reduction in peak sodium current, 69% reduction in L-type calcium current
and a reduction of 70% and 80% in potassium currents 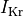 and
and 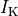 , respectively.
In the model these modifications are implemented by altering the peak conductivities of the respective currents as follows:
, respectively.
In the model these modifications are implemented by altering the peak conductivities of the respective currents as follows:
# all modification strings yield the same results
bench --imp TT2 --imp-par="GNa-62%,GCaL-69%,Gkr-70%,GK1-80%" --numstim 10 --bcl 500 --duration 5000
# or
bench --imp TT2 --imp-par="GNa*0.38,GCaL*0.31,Gkr*0.3,GK1*0.2" --numstim 10 --bcl 500 --duration 5000
To make sure that the provided parameter modifications are used as expected look at the log messages printed to the console. You should see messages confirming the use of the specified parameter modifications:
Ionic model: TT2
GNa modifier: -62% value: 5.63844
GCaL modifier: -69% value: 1.2338e-05
Gkr modifier: -70% value: 0.0459
GK1 modifier: -80% value: 1.081
To observe the effect of the modification relative to the baseline model simulate a train of action potentials with both baseline and modified model. Run
# run baseline model
bench --imp TT2 --numstim 10 --bcl 500 --duration 5000 --fout=TT2_baseline
# run modified PZ model
bench --imp TT2 --imp-par="GNa-62%,GCaL-69%,Gkr-70%,GK1-80%" --numstim 10 --bcl 500 --duration 5000 --fout=TT2_PZ
Fig. 37 illustrates the effect of the parameter modifications upon AP features.
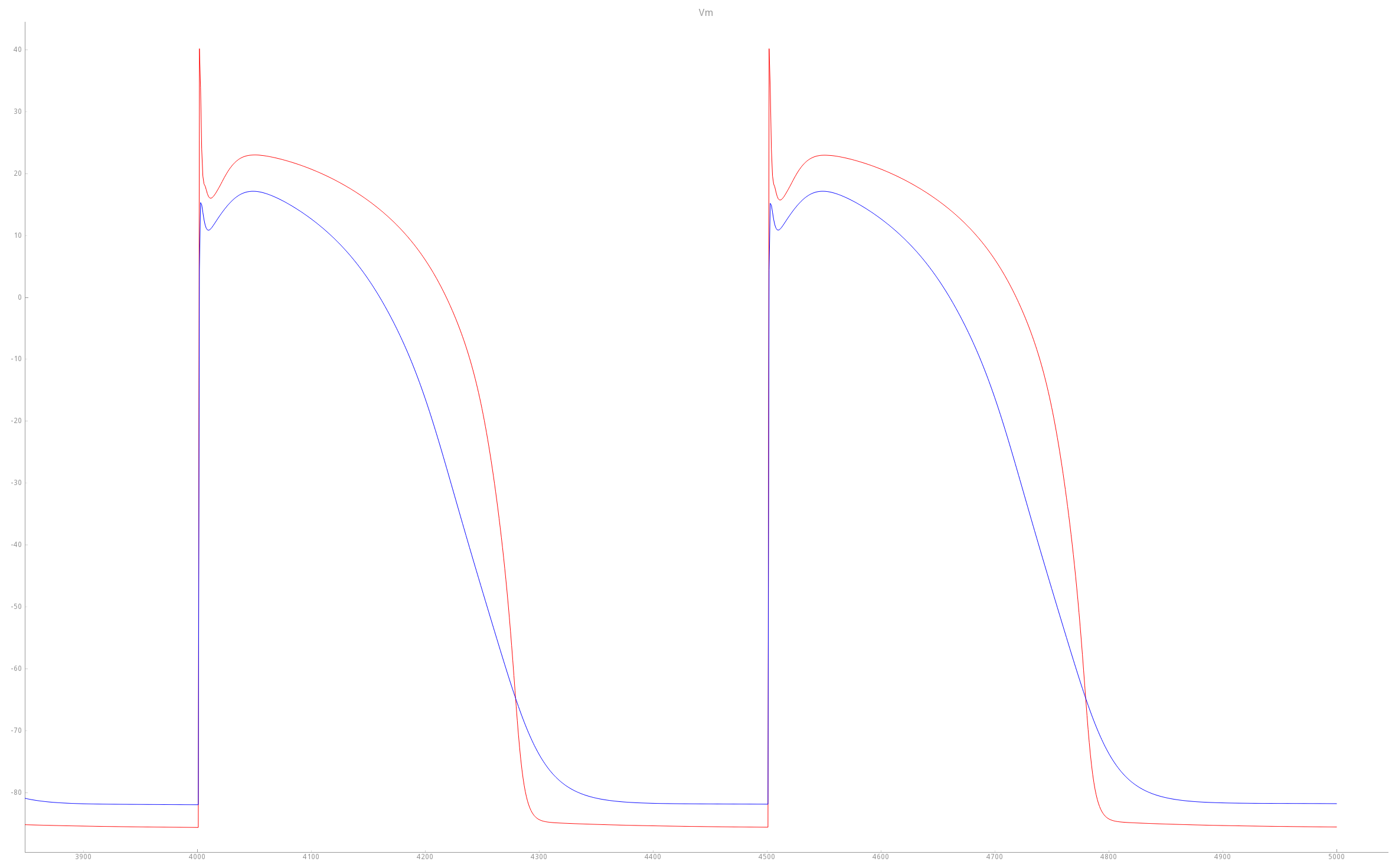
Fig. 37 Comparison of TT2 APs with baseline (red trace) and modified PZ (blue trace) settings. As a result of the modifications, the PZ APs feature a longer duration, decreased upstroke velocity and decreased peak amplitude compared to baseline APs.
Model augmentation
Published models of cellular dynamics are not complete and comprehensive representations
of the electrophysiological behavior of a myocyte.
Rather, the represent a subset of features which were deemed relevant for a given purpose.
This is true for any published model, none of them is able to represent myocyte behavior
under an arbitrary range of experimental circumstances.
For the sake of verification it is crucial to be able to run models
under the exact same conditions under which published results were obtained.
However, after verification it is often necessary to augment a model with additional features
which remained unaccounted for in the original publication.
The --plug-in mechanism is designed for such applications
where additional currents or physical effects such as the generation of active tension are considered
without recompiling or directly modifying the model as published.
The underlying concept is illustrated in Fig. 38.
Typical augmentation is used for incorporating additional currents which play a role
when driving the transmembrane potential 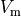 beyond the physiological range
during the application of a strong depolarizing/hyperpolarizing stimuli
such as an electroporation current, EP,
an electroporation current with pore resealing, EP_RS,
or a hypothetical time-independent outward rectifying potassium current IA,
or to account for the effect of adrenergic stimulation by incorporating
an acetylcholine-dependent potassium current I_ACh
beyond the physiological range
during the application of a strong depolarizing/hyperpolarizing stimuli
such as an electroporation current, EP,
an electroporation current with pore resealing, EP_RS,
or a hypothetical time-independent outward rectifying potassium current IA,
or to account for the effect of adrenergic stimulation by incorporating
an acetylcholine-dependent potassium current I_ACh

Fig. 38 Design concept underlying the implmented augmentation mechanism in LIMPET.
For instance, to augment a model of cellular dynamics to be used for studying the effect of defibrillation shocks,
one would activate the plugins EP_RS and IA.
This is achieved as follows:
bench --imp TT2 --plug-in "EP_RS:IA"
A frequent use of plugins is the augmentation with active stress models.
For instance, to specialize a human ventricular myocyte model for use in a ventricular electro-mechanical modeling study
one would enable an active stress model such as LandHumanStress:
bench --imp TT2 --plug-in "LandHumanStress"
As shown above in the Section on usage of –imp-par,
the default behavior of plugins can also be modified in the same way
as for the parent cell model. For instance, to reduce the peak force generated by 25 % one would use a plug-par string as follows:
bench --imp TT2 --plug-in "LandHumanStress" --plug-par="Tref-25%"
When using more than one plugin, parameter modification strings for the various plugins are separated by a :.
For instance, if we further augment with the ATP-sensitive potassium current I_KATP
and modify the 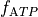
bench --imp TT2 --plug-in "I_KATP:LandHumanStress" --imp-par "GNa*0.8" --plug-par "f_ATP-10%:Tref-10%,TRPN_n+25%"
Again, a message is printed to the console confirming that the requested parameter modifications have been performed:
Ionic model: TT2
GNa modifier: *0.8 value: 11.8704
Plug-in: I_KATP
f_ATP modifier: -10% value: 0.00099
Plug-in: LandHumanStress
Tref modifier: -10% value: 108
TRPN_n modifier: +25% value: 2.5
Limit cycle
Action potentials and the trajectory of state variables depend on the basic cycle length
by which myocytes are activated.
Typically, a train of pacing pulses of a certain length are required
until the electrical activity in a myocyte arrives at a limit cycle,
that is, the transmembrane voltage 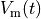 and all state variables
in the state vector
and all state variables
in the state vector 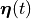 traverse the exact trajectory in the state space
after each perturbation with the same stimulus.
Mathematically, this boils down to
traverse the exact trajectory in the state space
after each perturbation with the same stimulus.
Mathematically, this boils down to
(5)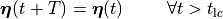
where 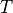 is the basic cycle length,
is the basic cycle length, bcl, and 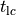 is an instant in time
beyond which we deem the time evolution of the state variables to follow a limit cycle.
In general, more recent ionic models, particularly those which allow intracellular ionic concentrations to vary,
are unlikely to arrive at a stable limit cycle.
Instead of demanding the exact same trajectories are traversed in each cycle
one could use various norms to demand that the beat-to-beat deviations in the state space
remain within a certain limit,
is an instant in time
beyond which we deem the time evolution of the state variables to follow a limit cycle.
In general, more recent ionic models, particularly those which allow intracellular ionic concentrations to vary,
are unlikely to arrive at a stable limit cycle.
Instead of demanding the exact same trajectories are traversed in each cycle
one could use various norms to demand that the beat-to-beat deviations in the state space
remain within a certain limit, 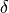 .
For instance, we could demand
.
For instance, we could demand
(6)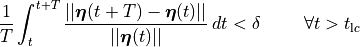
which would the relative difference between two cycles is, on average, less than a desired relative error 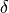 .
Under this norm it is still possible that relative differences exceed
.
Under this norm it is still possible that relative differences exceed
While using norms to detect the instant 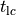 beyond which the state trajectories traverse a stable limit cycle
is certainly feasible, one has to keep in mind that various myocyte models will not arrive at a stable limit cycle
in the strict mathematical sense and that myocytes in vivo never operate in a regime
that would comply with such a rigorous constraint.
A more pragmatic approach is to determine
beyond which the state trajectories traverse a stable limit cycle
is certainly feasible, one has to keep in mind that various myocyte models will not arrive at a stable limit cycle
in the strict mathematical sense and that myocytes in vivo never operate in a regime
that would comply with such a rigorous constraint.
A more pragmatic approach is to determine 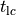 by visual inspection.
This is easily achieved with limpetGUI by pacing a cell for a sufficiently larger number of pacing cycles
and simply observe the envelope of all state time traces.
For the purpose of illustration an example is shown in Fig. 39 and Fig. 40.
by visual inspection.
This is easily achieved with limpetGUI by pacing a cell for a sufficiently larger number of pacing cycles
and simply observe the envelope of all state time traces.
For the purpose of illustration an example is shown in Fig. 39 and Fig. 40.
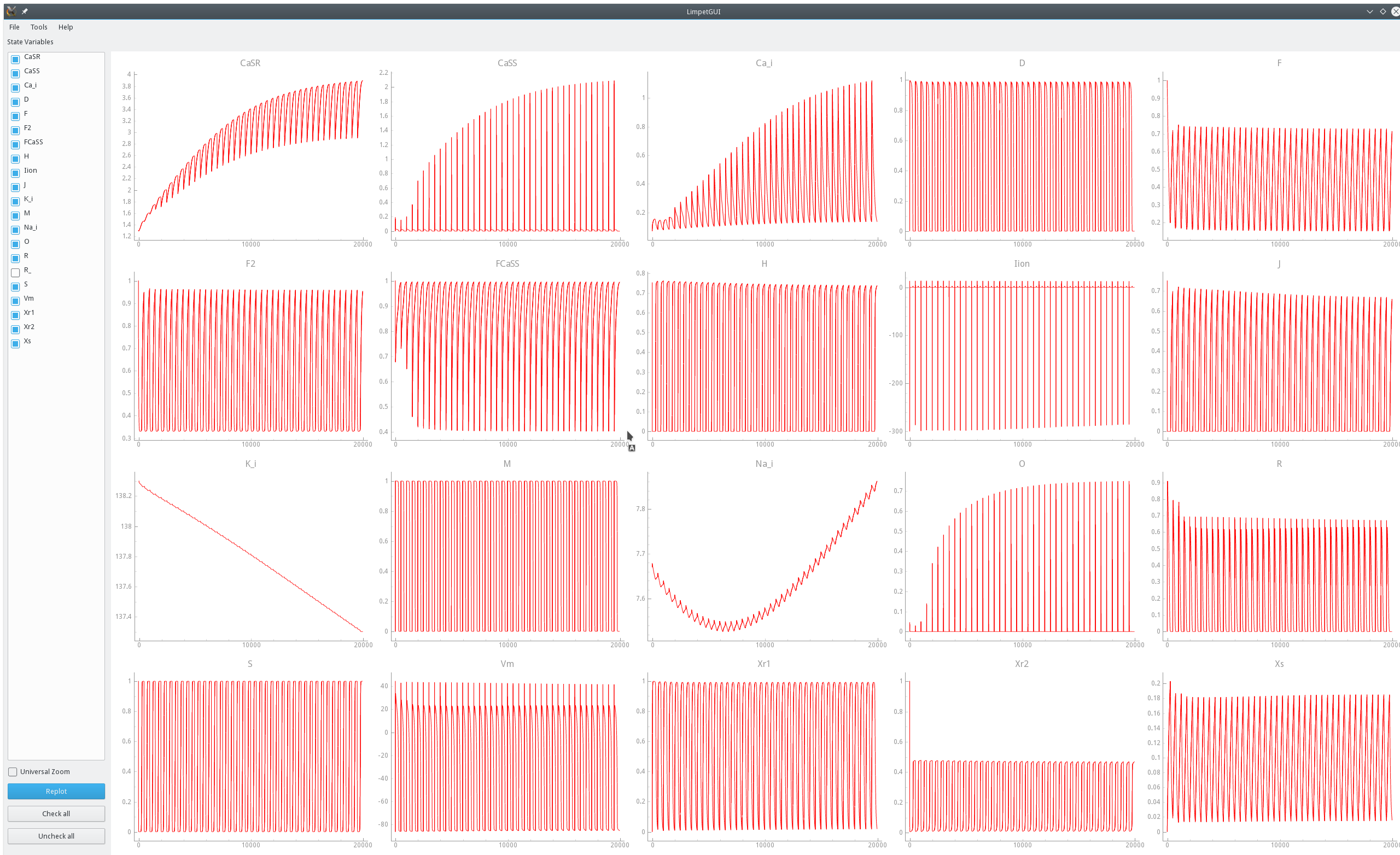
Fig. 39 Visualization of a limit cycle pacing experiment using limpetGUI. After 20 seconds pacing at a bcl of 500 ms most state variables settle in at a limit cycle with the exception of intracellular concentration of sodium and potassium ions.
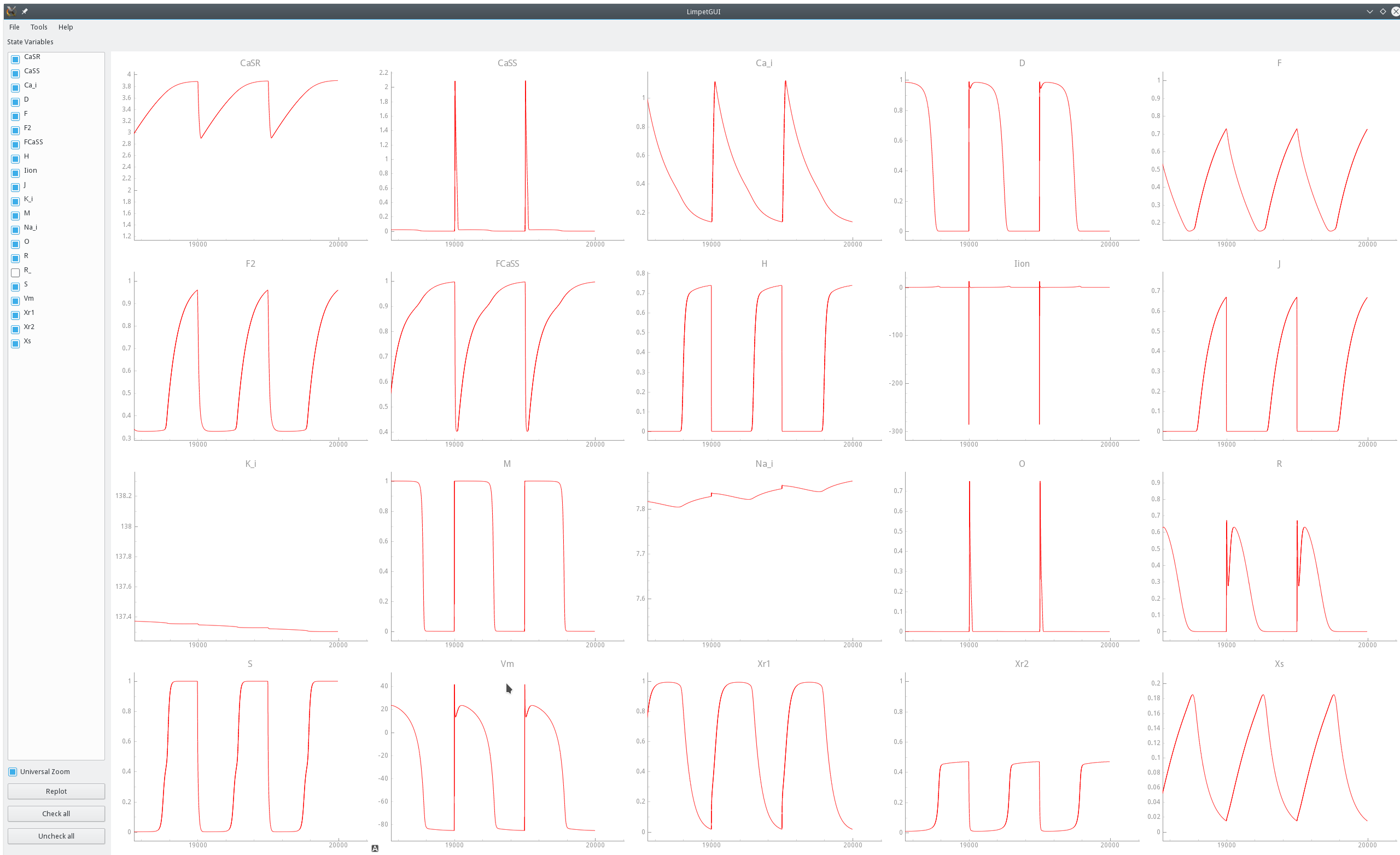
Fig. 40 Zoom on state traces over the last three pacing cycles of the same pacing experiments shown above in Fig. 39.
Initial state
Models of cellular dynamics are virtually never used with the values given for the initial state vector. Rather, cells are based to a given limit cycle to approximate the experimental conditions one is interested in. The state of the cell can be frozen at any given instant in time and this state can be reused then in subsequent simulations as initial state vector. Typically, the state of a cell is frozen in its limit cycle right at the end of the last diastolic interval. The standard procedure based on bench would proceed along the following steps:
Parameterize and augment a cell model corresponding to the experimental conditions of interest and for the intended application
Run bench then for a sufficiently large number of pacing pulses
numstimuntil a reasonable approximation of a stable limit cycle is achieved for the given cycle lengthbcl. Confirm the arrival at a limit cycle at least visually using limpetGUI.Store the initial state vector at the very end of the pacing protocol, that is, for
numstimstimuli and a givenbcldetermine the end time of the pacing protocol astsave = tstart + bcl*numstimSave the state vector at the determined time
tsaveinto a state vector file.
The last step of saving the state vector is triggered using the parameters --save-ini-time and --save-ini-file.
If we want to save the state of a myocyte after 25 pacing pulses at a basic cycle length of 500 ms
with the time of delivering the first pacing pulse at 0 ms one saves the initial state vector as follows:
# run baseline model
bench --imp TT2 --plug-in "LandHumanStress" --fout=TT2_baseline \
--stim-start 0. --numstim 25 --bcl 500 --duration 12500 \
--save-ini-time 12500 --save-ini-file TT2_lc_bcl_500_baseline.sv
# run modified PZ model
bench --imp TT2 --plug-in "LandHumanStress" --imp-par="GNa-62%,GCaL-69%,Gkr-70%,GK1-80%" --fout=TT2_PZ \
--stim-start 0. --numstim 25 --bcl 500 --duration 12500 \
--save-ini-time 12500 --save-ini-file TT2_lc_bcl_500_PZ.sv
These runs generate two state vector files, TT2_lc_bcl_500_baseline.sv and TT2_lc_bcl_500_PZ.sv
which store the state of each state variable at the instant t=12500 ms under the above given pacing protocol.
For instance, the state vector under baseline conditions in the file TT2_lc_bcl_500_baseline.sv
will be similar to:
-85.2262 # Vm
1 # Lambda
0 # delLambda
0.308053 # Tension
- # K_e
- # Na_e
- # Ca_e
0.00256503 # Iion
- # tension_component
TT2
0.126796 # Ca_i
3.62845 # CaSR
0.000380231 # CaSS
0.907029 # R_
2.68967e-07 # O
7.62609 # Na_i
137.689 # K_i
0.00172638 # M
0.743346 # H
0.678447 # J
0.0150679 # Xr1
0.470865 # Xr2
0.0143382 # Xs
2.43132e-08 # R
0.999995 # S
3.3857e-05 # D
0.729795 # F
0.959628 # F2
0.995618 # FCaSS
LandHumanStress
0.0249847 # TRPN
0.999196 # TmBlocked
0.000641671 # XS
8.33073e-05 # XW
0 # ZETAS
0 # ZETAW
0 # __Ca_i_local
Action Potential Duration (APD) Restitution Experiments
The single cell EP tool bench provides built-in capabilities for performing restitution experiments.
Restitution experiments with bench are steered through the following command line arguments
--restitute, --res-file and --res-trace.
--restitute
pick the protocol for performing the restitution experiment.
Possible values are "S1S2", "dyn" or "S1S2f".
--res-file
definition file for restitution parameters.
For a description of restitution file formats see :ref:`restitution protocol definition <restitution-protocol-def>`.
By default no restitution protocol defintion file is provided.
--res-trace
Can be on or off, toggles writing of trace files
Action potential analysis data are written in the following format:
#Beat Pre(P||*) lc APD(n) DI(n) DI(n-1) Tri VmMax VmMin
1 * 0 288.95 711.04 11.69 0.00 44.30 -86.08
2 * 0 286.97 713.02 711.04 0.00 45.27 -86.04
3 * 0 288.58 711.42 713.02 0.00 45.31 -86.01
4 * 0 304.53 695.00 711.42 78.29 45.37 -85.98
5 * 0 305.50 694.50 695.00 78.54 45.26 -85.95
6 * 0 305.90 694.10 694.50 78.74 45.31 -85.92
7 * 0 306.26 693.74 694.10 78.93 45.33 -85.90
8 * 0 306.59 693.40 693.74 79.11 45.20 -85.87
where the column headers refer to: #Beat - the total beat number in the protocol; Pre - whether beat was premature P or not ***; lc - whether AP traversed a limit cycle in the state space, 1, or not, 0; DI(n) - diastolic interval in ms of the current beat and DI(n-1) of the previous beat; Tri - Triangulation of the AP; VmMax and VmMin - maximum and minimum value of AP within pacing cycle.
Restitution data are written following the same format, but keeping only those beats which were marked as premature in the AP analysis file.
33 P 0 276.07 723.94 180.25 85.35 41.02 -85.58
46 P 0 272.73 727.27 170.63 85.93 40.11 -85.53
59 P 0 268.79 731.22 161.30 86.36 39.19 -85.49
72 P 0 264.53 735.47 151.97 86.84 38.27 -85.46
85 P 0 259.94 740.07 142.59 87.34 37.29 -85.43
98 P 0 255.01 744.99 133.16 87.94 36.20 -85.40
111 P 0 249.66 750.35 123.70 88.61 35.02 -85.37
124 P 0 243.87 756.14 114.14 89.45 33.68 -85.35
137 P 0 237.56 762.45 104.56 90.45 32.18 -85.32
150 P 0 230.68 769.32 94.94 91.71 30.47 -85.30
For an introduction into using bench as a tool for measuring restitution curves see the restitution experiments in the tutorials.
Code Generation
A tutorial on using the code generation tool limpet_fe.py is given here.