Tissue Scale

Passive Material Models

Holzapfel and Ogden (2009) myocardial model

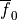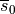The ventricular myocardium model is a non-linear, hyperelastic, nearly incompressible and orthotropic material with a layered organization of myocytes and collagen fibers that is characterized by a right-handed orthonormal set of basis vectors. 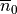These basis vectors consist of the fiber axis $\overline{f}_0$ , which coincides with the orientation of the myocytes, the sheet axis $\overline{s}_0$ and the sheet-normal axis $\overline{n}_0$ .

Comparing to experimental data Holzapfel and Ogden reduced a constitutive law with the full set of invariants to a simplified model which combines the volumetric part, an isotropic Demiray part, two fiber parts and one fiber interaction part:

$\Psi(\boldsymbol{C}) = \frac{\kappa}{2}\ln(J)^2 + \frac{a}{2b} \left\{ \exp\left[b(\overline{I}_1-3)\right]-1 \right\} + \sum_{i=\mathrm{f,s}} \left[\frac{a_i}{2b_i}\left\{\exp\left[b_i (\overline{I}_i-1)^2\right]-1\right\}\right] + \frac{a_\mathrm{fs}}{2b_\mathrm{fs}} \left\{ \exp\left[b_\mathrm{fs}\overline{I}_\mathrm{fs}^2\right]-1 \right\}$

with invariants

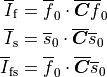
$\overline{I}_\mathrm{f} &= \overline{f}_0\cdot\overline{\boldsymbol{C}}\overline{f}_0 \\ \overline{I}_\mathrm{s} &= \overline{s}_0\cdot\overline{\boldsymbol{C}}\overline{s}_0 \\ \overline{I}_\mathrm{fs}&= \overline{f}_0\cdot\overline{\boldsymbol{C}}\overline{s}_0$

and parameters

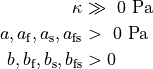
$\kappa &\gg \text{ 0 Pa} \\ a, a_\mathrm{f}, a_\mathrm{s}, a_\mathrm{fs} &> \text{ 0 Pa} \\ b, b_\mathrm{f}, b_\mathrm{s}, b_\mathrm{fs} &> 0$

The default parameters are

a	b	a_f	b_f	a_s	b_s	a_fs	b_fs	kappa	Data
0.345	9.242	18.54	15.97	2.564	10.45	0.417	11.60	1000	Dog

Guccione et al. myocardial model

The passive behavior of myocardial tissue is modeled by a nearly-incompressible, transversely isotropic Fung-type constitutive law, first described by Guccione1991Passive and later also by Costa1996Three. 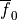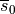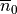The layered organization of myocytes and collagen fibers in the myocardium is characterized by a right-handed orthonormal set of basis vectors consisting of the fiber axis $\overline{f}_0$ , which coincides with the orientation of the myocytes, the sheet axis $\overline{s}_0$ and the sheet-normal axis $\overline{n}_0$ .

The strain-energy function is given by

$\Psi(\boldsymbol{C}) = \frac{\kappa}{2} \left( \log\,J \right)^2 + \frac{a}{2}\left[\exp(\overline{Q})-1\right],$

where

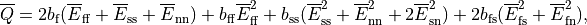
$\overline{Q} = 2b_\mathrm{f}(\overline E_\mathrm{ff} + \overline E_\mathrm{ss} + \overline E_\mathrm{nn}) + b_\mathrm{ff} \overline E_\mathrm{ff}^2 + b_\mathrm{ss} (\overline E_\mathrm{ss}^2 + \overline E_\mathrm{nn}^2 + 2\overline E_\mathrm{sn}^2) + 2b_\mathrm{fs}(\overline E_\mathrm{fs}^2 + \overline E_\mathrm{fn}^2),$

and

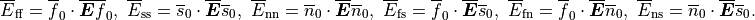
$\overline E_{\mathrm{ff}}=\overline{f}_0\cdot\overline{\boldsymbol{E}}\overline{f}_0,\ \overline E_{\mathrm{ss}}=\overline{s}_0\cdot\overline{\boldsymbol{E}}\overline{s}_0,\ \overline E_{\mathrm{nn}}=\overline{n}_0\cdot\overline{\boldsymbol{E}}\overline{n}_0,\ \overline E_{\mathrm{fs}}=\overline{f}_0\cdot\overline{\boldsymbol{E}}\overline{s}_0,\ \overline E_{\mathrm{fn}}=\overline{f}_0\cdot\overline{\boldsymbol{E}}\overline{n}_0,\ \overline E_{\mathrm{ns}}=\overline{n}_0\cdot\overline{\boldsymbol{E}}\overline{s}_0.$

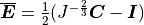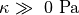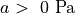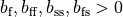with $\overline{\boldsymbol{E}} = \frac{1}{2}(J^{-\frac{2}{3}}\boldsymbol{C}-\boldsymbol{I})$ the modified isochoric Green–Lagrange strain tensor. The bulk modulus $\kappa \gg \text{ 0 Pa}$ serves as a penalty parameter to enforce nearly incompressibility and $a >\text{ 0 Pa}$ is a stress-like scaling parameter. All other parameters $b_\mathrm{f}, b_\mathrm{ff}, b_\mathrm{ss}, b_\mathrm{fs} > 0$ are dimensionless and negative values are not physically acceptable. Default parameters are:

a	b_ff	b_ss	b_nn	b_fs	b_fn	b_ns	kappa	Data
0.876	18.48	3.58	3.58	3.58	1.627	1.627	1000	Dog

and were fitted to produce epicardial strains that were measured previously in the potassium-arrested dog heart.

Several modifications of the original model were published, most notably the simplified version due to Omens1993Measurement and Guccione1995Finite

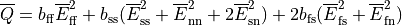
$\overline{Q} = b_\mathrm{ff}\overline E_\mathrm{ff}^2 + b_\mathrm{ss} (\overline E_\mathrm{ss}^2 + \overline E_\mathrm{nn}^2 + 2\overline E_\mathrm{sn}^2) + 2b_\mathrm{fs}(\overline E_\mathrm{fs}^2 + \overline E_\mathrm{fn}^2)$

This is also the version that is implemented in CARP. The parameters are then reduced to:

a	b_ff	b_ss	b_fs	kappa	Data
0.876	18.48	3.58	1.627	1000	Dog

Mechanical Boundary Conditions

The definition of mechanical boundary conditions follows the same basic concept as is used for defining electrical stimuli. First, a region of the mesh is defined, typically a set of surface nodes or faces, to which boundary conditions are applied. Subsequently, the quantity to apply and its time course is defined. These quantities in mechanics simulations are either a scalar pressure (Neummann boundary conditions), or vector displacements (Dirichlet boundary conditions).

The definition of mechanical boundary conditions uses an analog approach to the definition of electrical stimuli. A complete definition of a mechanical boundary condition comprises two components, the definition of the boundary (in terms of vertices or surface elements) and the loading protocol. Mechanical loading protocols are described as time traces describing the time course of applied (scalar) pressure in the case of Neumann boundary conditions or (vectorial) displacements in the case of Dirichlet boundary conditions. The definition of Neumann and Dirichlet boundary conditions is very similar with the major difference being the use of the keyword mechanic_nbc[] for Dirichlet boundaries, and mechanic_nbc[] for Neumann boundaries.

Geometry definition: Boundary geometries can be defined in two ways, indirectly by specifying a volume within which all mesh nodes are considered then to be part of this boundary, or, explicitly, by providing a surface file containing all surface elements spanning the boundary.

The default definition is based on a block by specifying the lower left bottom corner and the lengths of the block along the Cartesian axes.

Tab. 12 Keywords used for definition of Neumann and Dirichlet boundary conditions
field	type	description
name	String	Identifier for electrode used for output (optional)
zd	Float	z-dimension of electrode volume
yd	Float	y-dimension of electrode volume
xd	Float	x-dimension of electrode volume
z0	Float	lower z-ordinate of electrode volume
y0	Float	lower y-ordinate of electrode volume
x0	Float	lower z-ordinate of electrode volume
ctr_def	flag	if set, block limits are [ x0 - xd/2 x0 + xd/2], othewise limits are [ x0 x0 + xd] etc

Alternatively, other types of region than blocks are available such as spheres, cylinders or, the most general case, list of finite elements. See the definition of tag regions for details. Electrodes can be defined then by assigning the index of a tag region to the geometry field:

Tab. 13 Alternative geometry definition based on tag regions
field	type	description
geometry	int	Index of region pre-defined in tag region array tagreg[]

An explicit definition of boundary conditions is also possible by providing a file holding the defining mesh entities. Here the formats between Neumann and Dirichlet boundaries is different, see below.

Tab. 14 Explicit definition of a Dirichlet boundary geometry using vertex files
field	type	description
vtx_file	String	File holding all nodal indices making up the boundary

Tab. 15 Explicit definition of a Neumann boundary geometry using surface file
field	type	description
surf_file	String	File holding all surface elements making up the boundary

Neumann Boundary Conditions

The definition of loading protocols differs between Neumann and Dirichlet boundaries due to the different physical quantities applied to the boundaries, i.e. scalar pressures always acting perpendicular to the Neumann boundary and vectorial displacement which can be enforced in any direction.

The Neumann loading protocol is defined based on two components, the time course of the applied load as defined in a trace file, and the magnitude of the load. Splitting of these two components offers the advantage of avoiding the redefinition of time traces for different magnitudes of loads.

Loading protocol definition: In the case of Neumann boundary conditions the time course and magnitude of applied pressures must be defined using the keywords summarized in Tab. 16.

Tab. 16 Definition of Neumann loading protocols
field	type	description
pressure	Float	pressure imposed on boundary in [kPa]
trace	File	trace file describing the time course of pressure

Dirichlet Boundary Conditions

Loading protocol definition: In the case of Dirichlet boundary conditions the time course and magnitude of applied displacements must be defined using the keywords summarized in Tab. 16.

Tab. 17 Definition of Dirichlet loading protocols
field	type	description
ux	Float	rate of displacement along x in [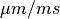 $\mu m/ms$ ]
uy	Float	rate of displacement along y in [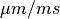 $\mu m/ms$ ]
uz	Float	rate of displacement along z in [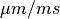 $\mu m/ms$ ]
ux_file	File	trace file describing time course of displacement ux
uy_file	File	trace file describing time course of displacement uy
uz_file	File	trace file describing time course of displacement uz
apply_ux	Flag	flag whether ux displacements are applied or not
apply_uy	Flag	flag whether uy displacements are applied or not
apply_uz	Flag	flag whether uz displacements are applied or not

In the Dirichlet case the definition of repetitive loading is also support. The definition follows analog to the definition of electrical stimulation protocols, re-using the same terminology, that is, a single sequence is referred to as a pulse and the duration of a single sequence is referred to as pacing cycle length or basic cycle length.

Tab. 18 Definition of repetitive Dirichlet loading protocols
field	type	description
start	float	time at which Dirichlet loading sequence begins
duration	float	duration of entire Dirichlet loading sequence
npls	int	number of pulses forming the sequence (default is 1)
bcl	float	basic cycle length for repetitive stimulation (npls > 1)

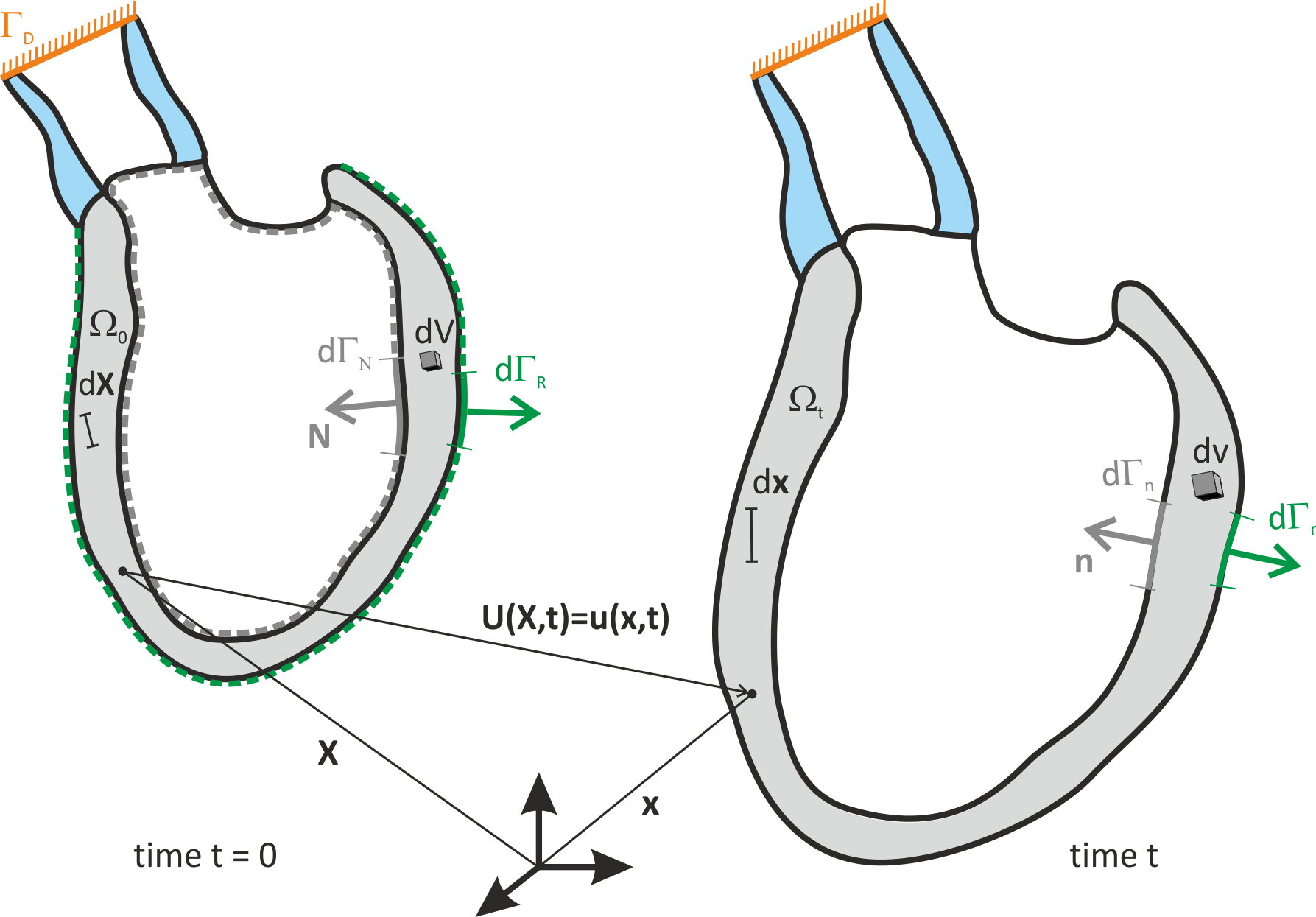
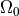Fig. 53 Deformation of an elastic body $\mathcal{B}$ from reference configuration $\Omega_{0}$ to the deformed configuration 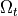$\Omega_{t}$ . Cardiac deformation is constrained by different types of boundary conditions. At the endocardial surface pressure imposes a Neumann boundary condition. The larger vessels are elastically anchored in the torso through the mediastinum which, in general, prevents larger displacements. Such boundary conditions can be approximated as a homogeneous Dirichlet boundary or, if image-based motion shall be applied to the model, as an inhomogeneous Dirichlet boundary. Boundary conditions at the epicardium are more complex due to the presence of the pericardium. Restraining forces at the epicardium can be approximated as a Robin boundary condition or, when coupled to a pericardial model, be represented as a mechanical contact problem.

A tutorial on how to apply mechanical boundary conditions in CARPentry simulations is given here.